이번 포스팅에서는 2017에 발표된 논문인 "Attention is all you need"에 수록된 Transformer를 살펴보겠습니다.
Transformer
Background
Transformer의 등장 배경은 두 가지의 장점을 계승하고, 한 가지의 단점을 보완하는데 있습니다.
직전 포스팅에서 살펴본 Bahdanau Attention, Luong Attention과 같은 Attention Mechanism이 잘 작동하고 있고, self-attention (Query, Key, Value의 출처가 같은 Attention)도 마찬가지로 Neural Translation Machine 영역에서 효과적이 었습니다. 또한 Seq2seq을 시작으로 Encoder-Decoder 구조로 Encoder로 Context를 추출하여 Decoder로 결과를 얻는 방식도 견고히 자리를 잡았습니다.
기존의 Attention Mechanism과 Encoder-Decoder 구조가 적용된 영역은 Recurrent Neural Network의 Framework위에서 작동했습니다. RNN-based 모델의 특징은 가중치를 공유하며, $t-1$ 스텝의 결과를 $t$에 순차적으로 적용하여 출력 값을 얻는 형태입니다. 때문에 Parallelization이 어렵고, 학습할 문장이 길어질 경우 memory를 많이 차지하는 문제가 발생합니다.Transformer는 위에서 언급한 두 장점을 취하고, 단점을 극복한 구조를 갖고 있습니다.가장 큰 변화는 RNN-based를 탈피하고 Feed Forward 방법을 택했다는 사실이고, RNN 처럼 문장의 순서를 반영하기 위하여 Positional Encoding을 이용했으며, Parallelization을 위하여 Multi-head Attetion을 도입한 것이 핵심입니다.
Overview of Transformer
Transformer가 전체적으로 어떤 구조를 가지고 있는지 살펴보고 하나씩 살펴보겠습니다.
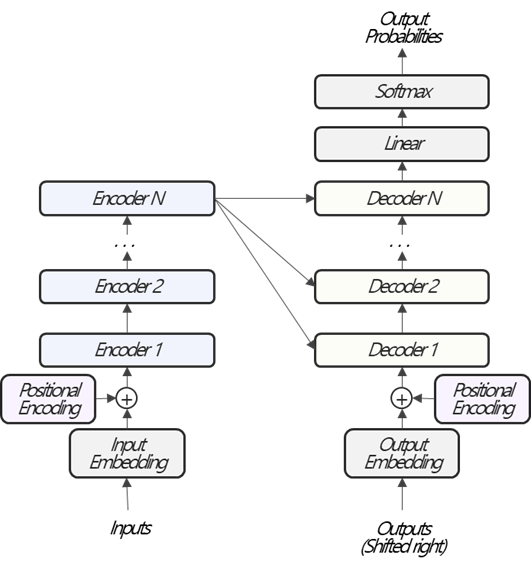
Transformer의 전반적인 구조는 Fig. 1과 같습니다. RNN-based 구조에서는 Input을 time-step에 따라 순차적으로 입력받지만, 위에서 언급한것 처럼 Transformer는 구조적인 한계를 극복하고자 한 번에 입력받습니다. 이렇게 되면, RNN-based 구조에서 time-step에 따라 순차적으로 입력받아 문장의 맥락을 고려할 수 없게되는 문제가 생깁니다. 이를 극복하고자 각 단어의 위치(순서) 정보인 Positional Encoding을 Input에 더해줍니다. 그 다음 Encoder, Decoder를 거쳐 Output를 생성하는 것은 기존의 Seq2seq 방법과 유사합니다.
RNN-based 구조처럼 Encoder와 Decoder는 세부구조를 가지고 있습니다.

Encoder와 Decoder의 내부구조는 조금 차이가 있습니다. 하지만 큰 틀에서는 Add&Norm Layer, Feed Forward Layer, Multi-Head Attention Layer, Masked Multi-Head Attention Layer, 총 4개의 Layer로 구성되어 있습니다. 위 그림에서 보이는 순서대로 Attention, Add&Norm, Feed Forward가 순차적으로 작동된다는 큰 그림을 알고서 이어지는 내용에서 각 모듈이 어떤 역할을 하는지 구체적으로, 그리고 순차적으로 살펴보겠습니다.
Inputs

Inputs에서는 문장을 입력받습니다. 해당 문장은 여러개의 단어로 구성되어 있고, 단어별로 embedding vector를 계산한 뒤, 순서대로 쌓아서 embedding matrix를 구성합니다. 이어질 설명의 편의를 위해 embedding vector의 크기를 $d_{model}$로 표기하며, 이는 원논문과 같습니다. I like an apple 이라는 문장을 예로 들어보겠습니다. 해당 문장은 I, like, an, apple, <eos>, 총 5개의 단어로 구성되어 있고, 각 단어의 embedding vector의 크기가 $d_{model}$이라고 했음으로 Input의 dimension은 $5\times d_{model}$이 됩니다. 여기까지는 RNN-based 구조와 동일합니다. 차이점은 Feeding하는데 있습니다.

RNN-based 구조에서는 단어별 Embedding Vector을 순차적으로 1-step, 1 vector를 입력 받는 방식이었습니다. Transformer의 경우 Embedding Vector를 stacking하여 matrix 형태로 입력받습니다. 때문에 Transformer의 입력 방식에는 단어의 위치를 반영을 할 수 없게 됩니다. 예를 들어 보겠습니다. "It is raining." , "I want it all."이라는 두 문장에서 it은 embedding 값이 같을 것입니다. Seq2Seq은 구조적으로 이 차이를 구분할 수 있지만, Transformer에서는 이를 구분할 방법이 없습니다. Transformer에서는 이를 구분하기 위해서 Positional Encoding 값을 더해 문장 순번에 같은 단어라도 문장에 등장하는 순번에 따라서 Embedding 값을 다르게 하는 방법을 취합니다.
Positional Encoding

Positional Encoding이란 위치 정보를 vector로 나타낸 값을 의미합니다. 정해진 위치 별로 고유값을 갖습니다. Transformer는 입력을 동시에 받아 순서/위치 정보를 반영할 수 없기 때문에 Positional Encoding을 입력 값에 더하여 고유의 Embedding 값을 갖도록 합니다.
기본적으로 Positional Encoding은 각 위치를 나타내는 값을 고유의 값을 가져야 합니다. 가령 첫 번째 자리의 값과 열 번째 자리의 값은 달라야한다는 의미입니다. 고유의 값을 갖는 다는 기본적인 특성과 더불어, Vaswani et al.은 토큰의 상대적인 위치를 학습할 수 있는 Positional Encoding을 적용하길 원했습니다. 때문에 $pos$에 대한 임의의 offset $k$에 대하여 $pos+k$는 $pos$의 linear function으로 표현가능한 것을 이용했습니다. 두 조건을 만족하는 Positional Encoding으로 다음을 적용합니다. $$\begin{align*}PE_{(pos, 2i)}&=\sin{\left(pos/10000^{2i/d_{model}}\right)}\\PE_{(pos, 2i+1)}&=\cos{\left(pos/10000^{2i/d_{model}}\right)}\end{align*}$$ 어떤 토큰이 주어지면 해당토큰은 위치정보인 $pos$와 $d_{model}$길이의 embedding vector를 갖습니다. 여기에서 $i$는 embedding vector내의 위치를 의미하고, $pos$는 토큰의 위치를 의미합니다. 또한 embedding vector의 위치가 짝수인 경우 sin함수를, 홀수인 경우 cos함수를 적용합니다. pos에 위치한 어떤 토큰의 positional encoding matrix는 다음과 같습니다. $$PE_{(pos)}=\begin{bmatrix}\sin{\left(pos\cdot f_{0}\right)}\\\cos{\left(pos\cdot f_{0}\right)}\\\sin{\left(pos\cdot f_{1}\right)}\\\cos{\left(pos\cdot f_{1}\right)}\\\vdots\\\sin{\left(pos\cdot f_{\frac{d_{model}-2}{2}}\right)}\\\cos{\left(pos\cdot f_{\frac{d_{model}-2}{2}}\right)}\end{bmatrix}$$여기에서 $f_{i}=1/10000^{2i/d_{model}}$입니다. pos가 고정된 상태에서 embedding 위치를 이동해보면, sin, cos 함수의 주기가 $2\pi$ 부터, $2\pi \cdot 10000$으로 뒤로 갈수록 주기가 길어지는 형태입니다.
Input 토큰들의 Embedding Matrix를, $E_{in}$, $(T_{in}\times d_{model})$라고 하면, Positional Encoding Matrix, $PE$는 같은 크기인 $(T_{in}\times d_{model})$의 크기를 갖습니다. 이어서 $E_{in}+PE$를 다음 Layer로 보냅니다. 여기서 $+$는 element-wise sum입니다.
Why Sinusoid?
위에서 설명한 positional encoding방법은 적어도 제 기준에서는 간단하진 않습니다. 앞에서 언급되었듯 Positional Encoding은 각 위치를 나타내는 고유값을 가져야하며, 추가적으로 Vaswani et al.은 토콘의 상대적인 위치가 학습가능한 방법을 적용하고자 했습니다.
위치정보를 표현할 수 있는 가장 간단한 방법은 각 토큰의 순서대로 자연수를 적용하는 것 입니다. 예를 들어 "I like an apple"이라는 문장이 있다면 I: 1/ like: 2/ an: 3/ apple: 4로 positional encoding하는 방법이 있습니다. 이 경우 두 가지 문제점이 있습니다. 첫 번째는 문장이 길어질 경우 무한히 큰 값이 입력되어 학습이 불안정해질 수 있습니다. 두 번째는 학습에 이용된 데이터 보다 긴 문장을 입력을 받을 경우 문제가 생깁니다. 즉 일반화가 어렵습니다.
다음으로 간단한 방법은 일반화를 위해 토큰의 위치를 0~1사이 값으로 표현하는 것 입니다. I: 0/ like: 0.33/ an: 0.66/ apple: 1로 나타낼 수 있습니다. 그런데 이방법의 경우 토큰의 개수에 따라서 각 위치의 encoding값이 바뀔 수 있습니다. 예를 들어 토큰이 3개라면, 두 번째 위치는 0.5값을 갖습니다. 즉, 각 위치별로 고유의 값을 갖지 않아 적용하기 어렵습니다.다음으로 생각해 볼 수 있는 것은 처음 언급된 방법을 10진수가 아닌 2진수로 나타내는 방법입니다.

위 그림에는 0~15에 해당하는 2진수 값이 있습니다. Binary로 나타내면 대부분의 수를 나타낼 수 있게되며, 일반화의 문제도 사라집니다. 하지만 긴문장을 대비하기 위해선 충분히 넉넉한 자리수가 필요하다는 단점이 있습니다. 2진수의 주기성을 이용하여 해당 문제를 해결할 수 있습니다. 2진수로 표기하면 규칙을 쉽게 발견할 수 있습니다. 첫 번째 자리수는 0, 1이 바뀌는 주기가 1이고, 두 번째 자리수는 주기가 2, 세 번째는 4, 네 번째는 8로 자리수가 커질 수록 0, 1이 바뀌는 주기가 길어집니다. 다시 positional encoding으로 돌아 와보면, 고유값을 갖고, 일반화 시킬 수 있으면 되니 0, 1일 필요는 없고, 자리 수가 커질 수록 주기가 길게 표현하기만 하면되는데, 이는 sinusoid로 해결 할 수 있습니다.
Vaswani et al., 2017에서 적용한 Positional Encoding은 토큰의 상대적인 위치가 학습 가능합니다. 즉, $pos$에 대한 임의의 offset $k$에 대하여 $pos+k$는 $pos$의 linear function으로 표현가능합니다. $PE_{pos}$는 sin, cos의 쌍으로 구성되어 있는데 한 쌍을 살펴보겠습니다. $$\begin{bmatrix}\alpha_{1}&\alpha_{2}\\\alpha_{3}&\alpha_{4}\end{bmatrix}\cdot\begin{bmatrix}\sin{\left(pos\cdot f_{i}\right)}\\\cos{\left(pos\cdot f_{i}\right)}\end{bmatrix}=\begin{bmatrix}\sin{\left((pos+k)f_{i}\right)}\\\cos{\left((pos+k)f_{i}\right)}\end{bmatrix}$$위 식을 만족시키는 $M$은 삼각 함수 덧셈 정리를 이용하면 찾을 수 있고, 다음과 같습니다. $$M=\begin{bmatrix}\cos{\left(k\cdot f_{i}\right)}&\sin{\left(k\cdot f_{i}\right)}\\-\sin{\left(k\cdot f_{i}\right)}& \cos{\left(k\cdot f_{i}\right)}\end{bmatrix}$$행렬 M은 모든 pos에서 찾을 수 있고, offset은 linear function으로 표현가능합니다.
Summary
Transformer 내용이 길어 포스팅을 나누어서 진행하려고 합니다. 이번 포스팅에서는 Transformer의 전체적인 그림과 지향점에 대해서 살펴보았습니다. 또한 Transformer의 여러 모듈중 초기 input을 처리하는 Input 방법과 핵심 역할을 하는 Positional Encoding을 살펴보았습니다. 긴 글 읽어주셔서 감사합니다:)
References
Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems. 2017.
https://kazemnejad.com/blog/transformer_architecture_positional_encoding/
https://wikidocs.net/31379
https://skyjwoo.tistory.com/entry/positional-encoding%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80
'Deep Learning > Attention Mechanism' 카테고리의 다른 글
| Transformer (2) (0) | 2022.02.21 |
|---|---|
| Luong Attention (0) | 2021.12.09 |
| Bahdanau Attention (0) | 2021.11.24 |



댓글