이번 포스팅에서는 Long Short-Term Memory (LSTM)에 대하여 작성하고자 합니다. LSTM은 이전 포스팅에서 다룬 RNN의 발전된 형태입니다. RNN 구조의 큰 특징은 과거의 정보를 은닉층에 저장하는 것인데, Bengio et al., 1994에 Long-term dependency 문제로 과거의 정보를 충분히 활용할 수 없음을 알게되었습니다. 위 RNN의 단점을 보안한 모형 LSTM을 Hochreciter et al., 1997이 제안합니다. 먼저 Long-term dependency 문제가 어떤 것인지 살펴보고 LSTM의 구조와 작동원리에 대해서 살펴보도록 하겠습니다.
The Problems of Long-term Dependencies
장기의존성 문제(the problems of long-term dependencies)는 은닉층의 과거의 정보가 마지막까지 전달되지 못하는 현상을 의미합니다.

은닉층의 값이 어떻게 계산되었는지 다시 살펴보겠습니다. $$h^{(t)}=\tau\left(Ux^{(t)}+Wh^{(t-1)}\right)$$ $t-2$시점까지 한 번 더 풀어써보겠습니다. $$h^{(t)}=\tau\left[Ux^{(t)}+W\tau(Ux^{(t-1)}+Wh^{(t-2)})\right]$$ 눈치채셨겠지만, $h^{(t)}$가 tangent hyperbolic(tanh), $\tau$에서 반복적으로 곱해집니다. 그런데 $\tau(\cdot)\in(-1,1)$입니다. 즉, 1보다 작은 값이 반복적으로 곱해지기 때문에, feed-forward의 관점에서는 뒷 단으로 갈 수록 앞의 정보를 충분히 전달할 수 없고, back-propagation의 관점에서는 tanh의 함수의 기울기가 0에 가깝거나 굉장히 큰 값이 발생할 수 있어, 기울기 소실 혹은 폭팔의 문제를 일으킵니다. (tanh 함수에 대한 내용은 이곳에 자세히 작성해두었습니다.)
조금 직관적인 예제를 하나 살펴보고 장기의존성문제를 확실히 이해할 수 있습니다. (이곳 블로그의 예제를 참조하였습니다.) 예를 들어, "The clouds are in the sky." 해당 문장의 'sky'를 RNN으로 예측하는 모형을 고려하면, input으로 'the', 'clouds', 'are', 'in' , 'the'까지 살펴보면 sky가 마지막에 온다는 사실은 쉽게 받아들일 수 있습니다. 그런데 "I grew up in France and want to be a plumber who the best is in the world and I speak fluent French." 이란 문장의 'French' 예측하기 위해선 문장 앞단의 'France'가 핵심역할을 할 것입니다. 하지만 'I', 'grew', 'up', 'in', 'France', 'and', ..., 'fluent'를 거쳐야 하고, 'France'가 너무 초반에 등장하여 뒷단까지 충분히 전달되기 어려워, 'French'로 예측하기가 쉽지 않습니다. 이러한 문제를 장기의존성문제라고 합니다.
안타깝게도 RNN에서는 장기의존성문제를 해결하기 힘들다고 합니다. (Bengio et al., 1994) 반면 다행히도 LSTM에서는 기본 RNN 구조에 몇가지 장치를 추가했고, 그래서 장기의존성문제가 발생하지 않습니다. LSTM에서 어떤 장치를 추가하여 장기의존성문제를 해결했는지 살펴 보겠습니다.
Long Short-Term Memory (LSTM)
LSTM 개요
LSTM은 RNN의 특별한 구조로 장기의존성을 학습할 수 있는 딥러닝 프레임워크입니다. LSTM은 Hochreiter et al., 1997에 의해 최조 제안되었습니다. LSTM을 이해하기 위해서 이전 포스팅에서 다루었던 RNN의 은닉층 계산 과정을 나타내면 아래 그림과 같습니다.

RNN은 단순히 이전 은닉층 값 $h^{(t-1)}$과 현재 입력 $x^{(t)}$에 각각 가중치를 곱하고 tanh 함수에 넣은 출력 값을 해당 순번, $t$의 은닉층 값 $h^{(t)}$로 계산하는 과정을 반복했습니다. 같은 맥락의 그림으로 LSTM의 은닉층 계산과정을 나타내면 다음과 같습니다.

조금 복잡해 보일 것 같습니다. (사실 복잡합니다...) 하지만 LSTM이 장기의존성문제를 해결하기 위한 구조라는 것을 유념하고 단계단계 살펴보면 쉽게 이해할 수 있습니다. LSTM의 은닉층에서 출력층으로 넘어가는 연산은 RNN과 상동합니다. 은닉층이 계산되는 과정을 단계 단계 살펴 보겠습니다.
LSTM의 핵심 아이디어

LSTM의 핵심 아이디어는 이전 단계의 정보를 memory cell에 저장하여 흘려보내는 것입니다. 현재 시점의 정보를 바탕으로 과거의 내용을 얼마나 잊을지 곱해주고, 그 결과에 현재의 정보를 더해서 다음 시점으로 정보를 전달합니다. 그러면 이어서 어떤 것을 곱하고, 더해주는지 자세히 살펴보도록 하겠습니다.
LSTM 작동 원리
1. 망각게이트 (Forget Gate)
LSTM의 첫 단추는 망각게이트로 과거의 정보를 얼마나 잊을지 결정하는 게이트입니다. 현시점의 정보와 과거의 은닉층의 값에 각각 가중치를 곱하여 더한 후 sigmoid 함수를 적용하여, 그 출력 값을 직전 시점의 cell에 곱해줍니다. sigmoid 함수의 값은 $(0, 1)$ 사이 값을 갖습니다. 이에 따라 1에 가깝다면 과거 정보를 많이 활용할 것이고, 0에 가깝다면 과거 정보를 많이 잃게됩니다.
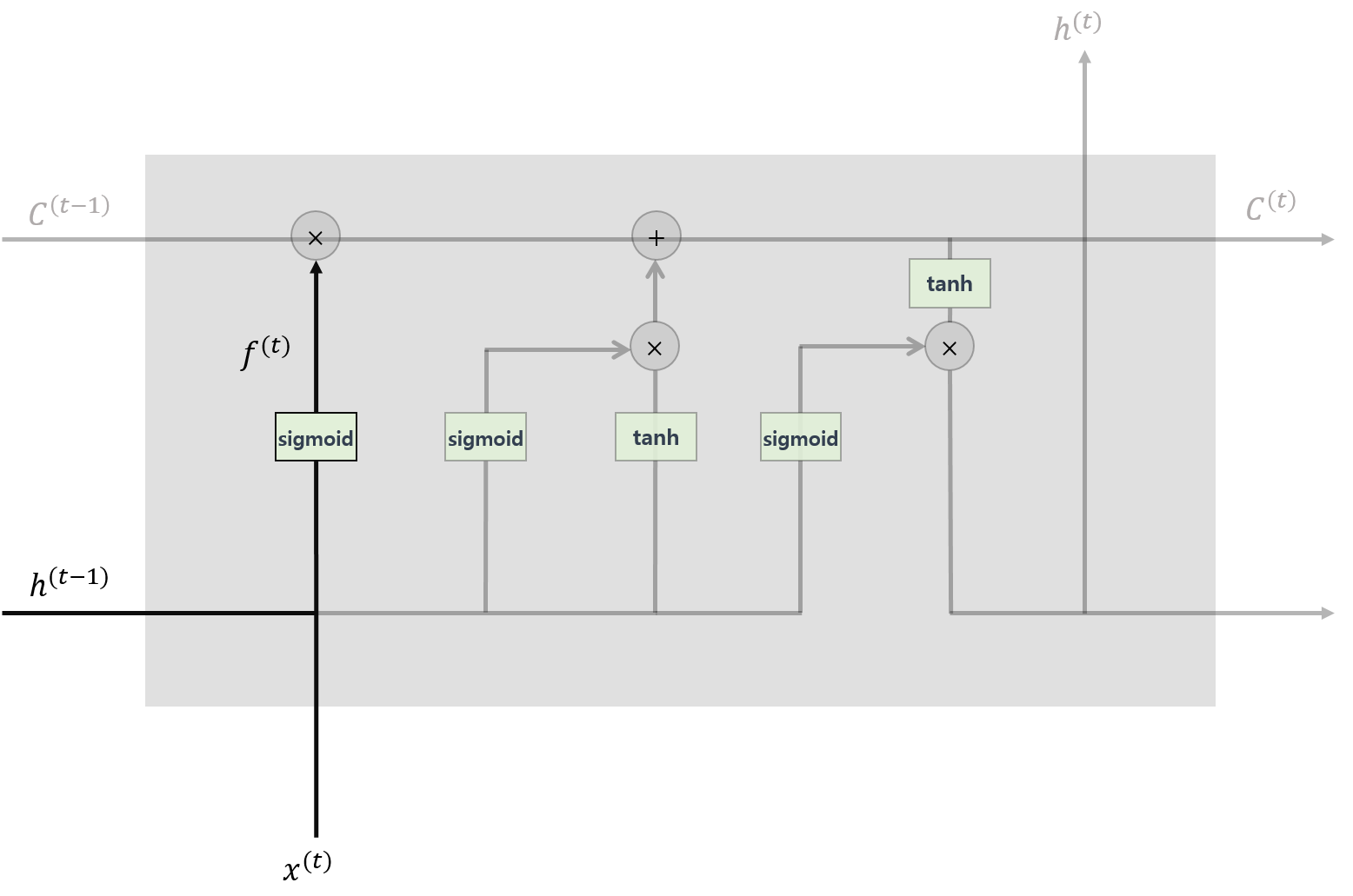
수식으로 정리하면 다음과 같습니다. $$f^{(t)}=\sigma\left(U_{f}x^{(t)}+W_{f}h^{(t-1)}\right)$$
2. 입력게이트 (Input Gate) & 입력후보 (Candidate)
다음 단계는 현시점의 정보를 셀에 입력할 크기를 정해주는 입력게이트와 현시점의 정보를 계산하는 입력후보입니다. 즉 현시점이 실제로 갖고 있는 정보(입력후보)가 얼마나 중요한지(입력게이트)를 반영하여 셀에 기록하는 것입니다.

수식으로 정리하면 다음과 같습니다. $$\begin{align*}i^{(t)}&=\sigma\left(U_{in}x^{(t)}+W_{in}h^{(t-1)}\right)\\\tilde{C}^{(t)}&=\tau\left(U_{c}x^{(t)}+W_{c}h^{(t-1)}\right)\end{align*}$$
3. Memory Cell의 계산
다음은 앞에서 계산한 망각게이트, 입력게이트, 입력후보를 이용하여 memory cell에 저장하는 단계입니다.

먼저 과거의 정보를 망각게이트에서 계산 된 만큼 잊고, 현시점의 정보 후보에 입력게이트의 중요도를 곱해준 것을 더하여 현시점 기준 memory cell을 계산합니다. 이를 수식으로 나타내면 다음과 같습니다. $$C^{(t)}=f^{(t)}*C^{(t-1)}+i^{(t)}*\tilde{C}^{(t)}$$ 여기에서 $*$은 pointwise operation입니다.
4. 출력게이트 (Output Gate)
이제 마지막입니다! 계산된 현시점의 memory cell을 현시점의 은닉층 값으로 출력할 양을 결정하는 출력게이트입니다.
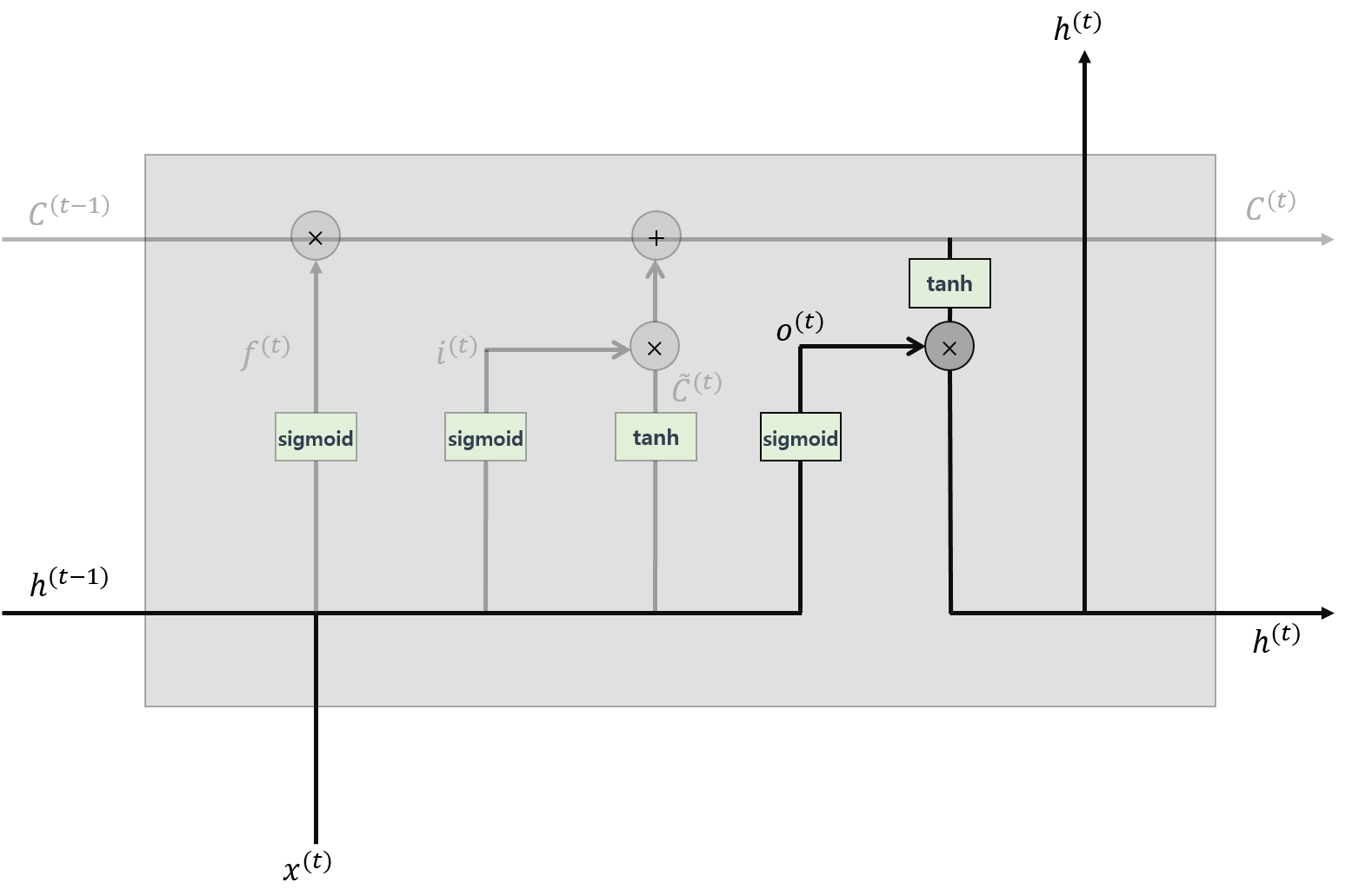
수식으로 나타내면 다음과 같습니다. $$\begin{align*}o^{(t)}&=\sigma\left(U_{o}x^{(t)}+W_{o}h^{(t-1)}\right)\\h^{(t)}&=o_{t}*\tau(C^{(t)})\end{align*}$$
5. 출력층
출력층 계산은 RNN과 동일합니다. 도안은 제시하지 않고 수식만 작성해보면 다음과 같습니다. $$\hat{y}^{(t)}=softmax\left(Vh^{(t)}\right)$$
LSTM 정리
위 5단계의 과정을 거치는 딥러닝 프레임워크가 LSTM입니다. LSTM의 작동과정은 다소 복잡하고 망각게이트, 입력게이트, 입력후보, 출력게이트를 계산하기 위한 가중치도 많습니다. LSTM의 작동과정을 조금 단순화 시킨 모형이 Gated Recurrent Unit (GRU)로 다음 포스팅에서 다루겠습니다.
마지막으로 위 모든 수식을 한 번에 정리하고 포스팅을 마치겠습니다. $$\begin{align*}f^{(t)}&=\sigma\left(U_{f}x^{(t)}+W_{f}h^{(t-1)}\right)\\i^{(t)}&=\sigma\left(U_{in}x^{(t)}+W_{in}h^{(t-1)}\right)\\\tilde{C}^{(t)}&=\tau\left(U_{c}x^{(t)}+W_{c}h^{(t-1)}\right)\\C^{(t)}&=f^{(t)}*C^{(t-1)}+i^{(t)}*\tilde{C}^{(t)}\\o^{(t)}&=\sigma\left(U_{o}x^{(t)}+W_{o}h^{(t-1)}\right)\\h^{(t)}&=o^{(t)}*\tau(C^{(t)})\\\hat{y}^{(t)}&=softmax(Vh^{(t)})\end{align*}$$

(이번 포스팅은 진짜 그림그리다... 죽을 뻔... 했습니다...ㅠㅠ)
References
- Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780.
- Bengio, Yoshua, Patrice Simard, and Paolo Frasconi. "Learning long-term dependencies with gradient descent is difficult." IEEE transactions on neural networks 5.2 (1994): 157-166.
- http://colah.github.io/posts/2015-08-Understanding-LSTMs/
'Deep Learning > Recurrent Neural Networks' 카테고리의 다른 글
| Seq2seq Model (Sequence to Sequence Model) (0) | 2020.04.20 |
|---|---|
| RNN Tensorflow + Keras (10) | 2019.12.07 |
| Gated Recurrent Units (GRU) (8) | 2019.08.15 |
| Recurrent Neural Networks (RNN) (0) | 2019.08.13 |




댓글