Word2vec

본 포스팅은 스탠포드 대학교 CS244n 강의 자료를 참고하여 작성되었습니다.

이전 포스팅에서는 SVD 기반 word embedding에 대해서 살펴보았습니다. 포스팅 말미에 SVD 기반 방법의 단점 몇 가지를 서술하며 Word2vec을 예고했습니다. 이번 포스팅에서는 Word2vec에 대해서 살펴보겠습니다.

Word2vec 개요

SVD 기반 모형에서는 대용량의 데이터를 계산하고 정보를 도출하는 방식을 취했습니다. 이에 따라 단어가 하나만 추가되더라도 많은 계산을 해야되는 단점이 있었습니다. 전체를 계산하는 것 대신, 어떤 계산을 한 번 반복할 때마다 가중치를 학습할 수 있고, 계속 반복하여 주어진 맥락(context)에 따른 단어(word)의 확률을 계산해나가는 방식을 Iteration based methods라고합니다.

Iteration based methods은 Y. Bengio et al.(2003)의 Neural Net Language Model (NNLM)에서 시작되어, 여기에 Recurrent Neural Nets을 결합하여 T. Mikolov et al.(2010)이 Recurrent Neural Net Language Model (RNNLM)을 발표합니다. 이어서 이번 포스팅에서 다루게 될 T. Mikolov et al.(2013)이 Word2vec을 발표합니다.  

Word2vec은 계산 효율이 좋고, 성능이 좋은 것으로 알려져있습니다. NLP에서는 학습하고자하는 단어(word)와 주변 단어, 즉 맥락(context)로 분류합니다. Word2vec은 학습할 word를 input으로 두느냐, output으로 두느냐에 따라서 CBOW와 Skip-Gram으로 분류됩니다.

• Continuous Bag Of Word (CBOW): 문장의 word를 input으로 하고, context를 output로 간주하여 학습하는 모형
• Skip-Gram: 문장의 context를 input으로 하고, word를 output으로 간주하여 학습하는 모형

CBOW와 Skop-Gram은 단순히 방향의 차이입니다. 이렇게 모형을 정의하고 나면 어떻게 학습할지가 다음 단계입니다. SVD 기반 방법의 단점 중 하나는 분석하고자 하는 데이터 word의 수가 많아지면 계산하기 힘들다는 점이었습니다. Word2vec에서 비슷한 문제가 발생하는데, 해당 단점을 해결하기 위하여 Negative Sampling, Hierarchical Softmax을 이용합니다.

• Negative Sampling: 단어 전체를 사용하지 않고 일부만 랜덤하게 선택하여 학습하는 방법
• Hierachical Softmax: 모든 단어를 고려하되, binary tree를 이용하여 출력층의 softmax 함수 계산을 최소화하는 방법

학습방법은 다음 포스팅에서 다루고, 이번 포스팅에서는 Word2vec의 CBOW와 Skip-gram에 대해서 살펴보겠습니다.

Language Models

Language model이란 문장 혹은 단어를 확률로 나타내는 모형을 말합니다. 우선 우린 $m$개의 word로 이루어진 문장을 다음과 같이 확률로 나타낼 수 있습니다. $$\mathbb{P}(w_{1},\cdots,w_{m})$$ 만약에 어떤 문장을 구성하는 단어가 완벽하게 독립이라고 가정한다면 우리는 위 모형을 다음과 같이 나타낼 수 있습니다. $$\mathbb{P}(w_{1},\cdots,w_{m})=\prod_{i=1}^{m}\mathbb{P}(w_{i})$$ 위 모형은 모든 단어가 완벽한 독립이라고 가정하고 1개 단어단위로 쪼갰는데 이를 Unigram model이라고 부릅니다. Unigram model은 사실 one-hot vector를 그대로 가지고 분석하는 것과 다름이 없으며, 문장을 구성하는 모든 단어가 독립이라고 가정하는 것 자체가 무리가 있습니다. 아주 자연스럽게 우리는 단어의 활용이 단순히 직전의 단어만, 다음에 나타날 단어에 영향을 준다고 생각해 볼 수 있습니다. 즉 2개의 단어 뭉치를 가지고서 모델링을 하면 $$\mathbb{P}(w_{1},\cdots,w_{m})= \mathbb{P}(w_{1})\prod_{i=2}^{m}\mathbb{P}(w_{i}|w_{i-1})\approx\prod_{i=2}^{m}\mathbb{P}(w_{i}|w_{i-1})$$로 나타낼 수 있으며, 이를 Bigram model 또는 Markov model이라고 부릅니다. 이를 일반화하여 단어 활용이 바로 직전 $n-1$개의 단어에만 의존하는 모형을 $$\mathbb{P}(w_{1},\cdots,w_{m})=\mathbb{P}(w_{1})\prod_{i=n}^{m}\mathbb{P}(w_{i}|w_{i-1},\cdots,w_{i-n})\approx\prod_{i=n}^{m}\mathbb{P}(w_{i}|w_{i-1},\cdots,w_{i-n})$$으로 나타낼 수 있으며, 이를 N-gram model이라고 합니다. 이때 $w_{i}$를 word라고, $w_{i-1},\cdots,w_{i-n}$을 context라고 부릅니다. Language Model 역시 단어의 수가 많아지면 계산량이 큽니다. 이어서 등장할 CBOW, Skip-Gram은 이러한 Language Model을 효율적으로 학습할 것인가에 대한 딥러닝 프레임워크로 받아들일 수 있습니다.

Continuous Bag Of Word model (CBOW)

CBOW는 word를 output으로, context를 input으로 사용하는 모형입니다. 즉, "The boy is going to school."이라는 문장을 고려했을 때, context size를 2로 했을 경우 'is'라는 word를 학습하기 위해 output으로 간주하고, 'The', 'boy', 'going', 'to'를 input으로 이용하는 모형이라는 말과 같습니다. 

Notation

• $x^{(c)}$: context에 대한 one-hot vector
• $y$: word에 대한 one-hot vector
• $\mathcal{V}\in\mathbb{R}^{n\times|V|}$: input에 곱해지는 행렬(input word matrix)
• $\mathcal{U}\in\mathbb{R}^{|V|\times n}$: output에 곱해지는 행렬(output word matrix)
• $|V|$: 전체 단어의 수
• $n$: embedding space를 정의하는 임의 크기

Framework for CBOW

Figure 1: CBOW Framework

1. (Input Layer) context에 대한 one-hot vector를 만들어 input에 넣습니다. context size를 $m$으로 했을 경우 $2m$개의 one-hot vector를 만들어 넣습니다. $$x^{(c-m)},\cdots,x^{(c-1)},x^{(c+1)},\cdots,x^{(c+m)}\in\mathbb{R}^{|V|}$$
2. (Input Layer → Hidden Layer) Input에 input word matrix를 곱해 값을 얻습니다. $$v_{c-m}=\mathcal{V}x^{(c-m)},\cdots,v_{c+m}=\mathcal{V}x^{(c+m)}\in\mathbb{R}^{n}$$
3. (Hidden Layer) 2의 결과를 평균내줍니다. $$\hat{v}=\frac{v_{c-m}+\cdots+v_{c+m}}{2m}\in\mathbb{R}^{n}$$
4. (Hidden Layer → Output Layer) 3의 결과를 output word matrix에 곱해 값을 얻습니다. $$z=\mathcal{U}\hat{v}\in\mathbb{R}^{|V|}$$
5. (Output Layer) 4에서 얻어진 score를 확률로 표현하기 위해 softmax 함수를 취합니다. $$\hat{y}=softmax(z)\in\mathbb{R}^{|V|}$$
6. (Loss) $\hat{y}$를 word의 one-hot vector인 $y$와 오차를 측정합니다.

CBOW 학습

학습의 과정은 deep learning과 같습니다. 내용이 익숙하지 않다면 여기에서 자세한 내용을 확인할 수 있습니다. 가볍게 학습에 대해서 설명을 이어가겠습니다. Cross-entropy loss, $\mathcal{L}$을 이용하여 오차를 측정하고 학습할 수 있습니다. $$\mathcal{L}(\hat{y},y)=-\sum_{j=1}^{|V|}y_{j}\log{\hat{y}_{j}}=-y_{i}\log{\hat{y}_{i}}$$ 학습할 word의 one-hot vector가 $i$번 째라고 하면, $i$ 번째 값만 1이고 나머진 0이기 때문에 위처럼 나타낼 수 있습니다. $\mathcal{V}$, $\mathcal{U}$의 모든 가중치의 집합을 $\theta$라고하면 CBOW는 다음을 푸는 것과 같습니다. $$\hat{\theta}=\underset{\theta}{\operatorname{argmin}}\mathcal{L}(\hat{y},y)$$ 이어서 $\mathcal{L}$을 자세히 살펴보겠습니다. $$\begin{align*}\mathcal{L}&=-\log{\mathcal{P}(w_{c}|w_{c-m},\cdots,w_{c+m})}\\&=-\log{\mathbb{P}(u_{c}|\hat{v})}\\&=-\log{\frac{exp(u_{c}^{\top}\hat{v})}{\sum_{j=1}^{|V|}exp(u_{j}^{\top}\hat{v})}}\\&=-u_{c}^{\top}\hat{v}+\log{\sum_{j=1}^{|V|}exp(u_{j}^{\top}\hat{v})}\end{align*}$$ Deep Learning과 마찬가지로 기울기 강하법으로 학습을 할 수 있습니다. 눈치채셨겠지만 $|V|$가 커지면 계산량이 굉장히 커집니다. 즉 softmax 함수를 계산하는데 문제점이 발생하는 것이고, 이를 해결하기 위한 방법으로 negative sampling, hierachical softmax 방법이 제안되었습니다. 두 방법은 다음 포스팅에서 자세히 다루겠습니다.

CBOW 예시

마지막으로 "The boy is going to school."의 'The'를 context size 2, CBOW로 학습하는 프레임워크를 확인하고 Skip-Gram으로 넘어가겠습니다.

Figure 2: CBOW 예시

Skip-Gram Model

Skip-Gram은 context를 input으로 word를 output로 이용하는 모형입니다.  즉, "The boy is going to school."이라는 문장을 고려했을 때, context size를 2로 했을 경우 'is'라는 word를 학습하기 위해 input으로 간주하고, 'The', 'boy', 'going', 'to'를 output으로 이용하는 모형이라는 말과 같습니다. 정확하게 CBOW와 input과 output을 반대로 사용합니다.

Notation

• $x$: word에 대한 one-hot vector
• $y^{(c)}$: context에 대한 one-hot vector
• $\mathcal{V}\in\mathbb{R}^{n\times|V|}$: input에 곱해지는 행렬(input word matrix)
• $\mathcal{U}\in\mathbb{R}^{|V|\times n}$: output에 곱해지는 행렬(output word matrix)
• $|V|$: 전체 단어의 수
• $n$: embedding space를 정의하는 임의 크기

Framework for Skip-Gram

 

Figure 3: Skip-Gram Framework

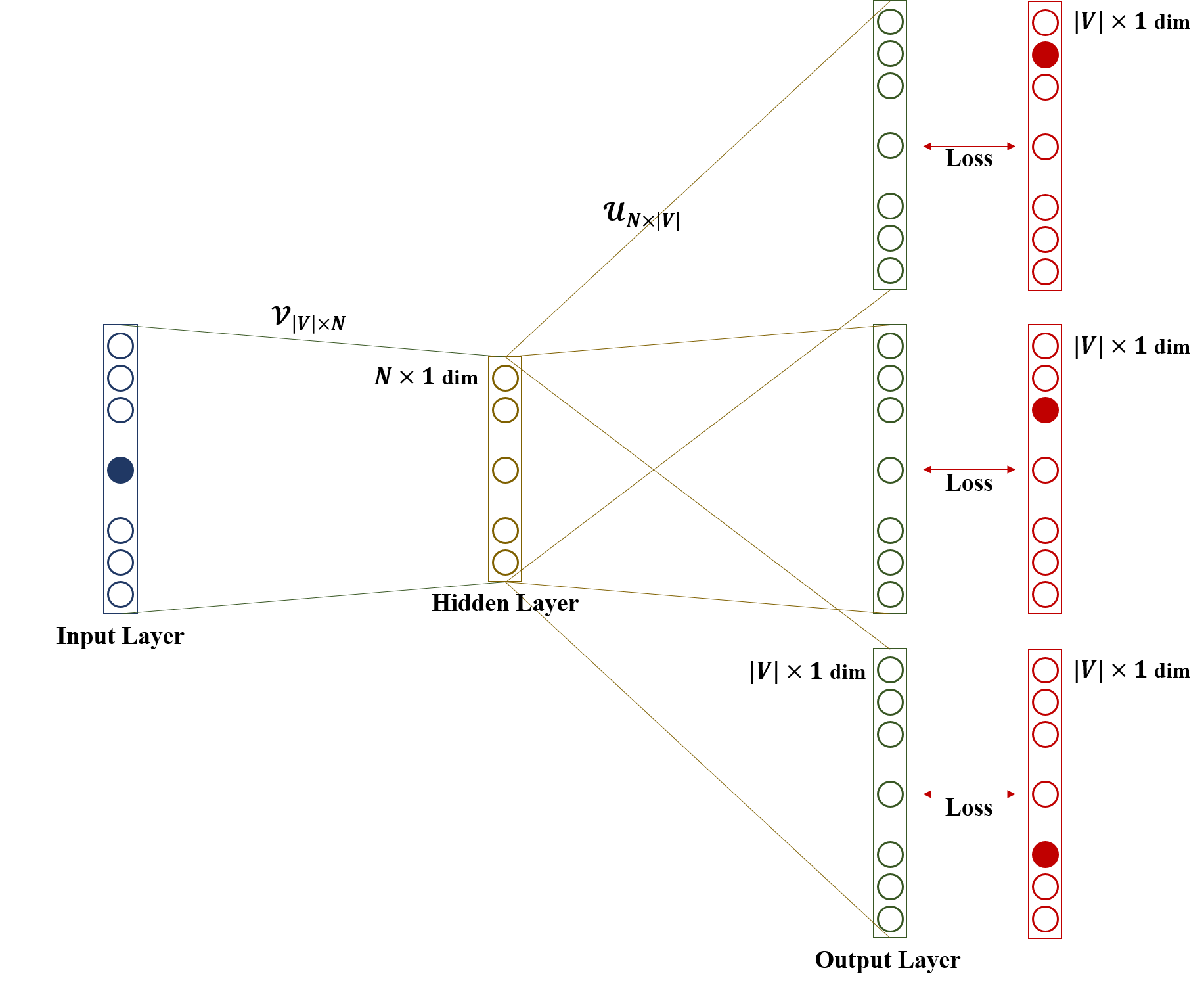
1. (Input Layer) word에 대한 one-hot vector를 만들어 input에 넣습니다. $$x\in\mathbb{R}^{|V|}$$
2. (Input Layer → Hidden Layer) Input에 input word matrix를 곱해 값을 얻습니다. $$v_{c}=\mathcal{V}x\in\mathbb{R}^{n}$$
3. (Hidden Layer → Output Layer) 2의 결과를 output word matrix에 곱해 값을 얻습니다. $$z=\mathcal{U}v_{c}\in\mathbb{R}^{|V|}$$
4. (Output Layer) 4에서 얻어진 score를 확률로 표현하기 위해 softmax 함수를 취합니다. $\hat{y}=softmax(z)\in\mathbb{R}^{|V|}$ 여기에서 $\hat{y}^{c-m},\cdots,\hat{y}^{c+m}$은 각 context의 확률 벡터로 해석할 수 있습니다.
5. (Loss) $\hat{y}$를 context의 one-hot vector인  각 $y^{(c)}$와 오차를 측정합니다.

Skip-Gram 학습

CBOW와 마찬가지로 cross-entropy loss를 이용하여 학습할 수 있습니다. $$\mathcal{L}(\hat{y},y)=-\sum_{j=0,j\ne m}^{2m}\sum_{k=1}^{|V|}y_{k}^{(c-j)}\log{\hat{y}_{k}^{(c-j)}}=-\sum_{j=0,j\ne m}^{2m}y^{(c-j)}\log{\hat{y}^{(c-j)}}$$ 여기에서 편의상 아래첨자를 뺀 것 $\hat{y}^{(c-j)}$, $y^{(c-j)}$을 $c-j$ 번 째 context의 one-hot encoding이 1인 위치의 값으로 약속하겠습니다. CBOW와 동일하게 $$\hat{\theta}=\underset{\theta}{\operatorname{argmin}}\mathcal{L}(\hat{y},y)$$으로 가중치를 학습할 수 있습니다. 이어서 $\mathcal{L}$을 자세히 살펴보겠습니다. $$\begin{align*}\mathcal{L}&=-\log{\mathbb{P}(w_{c-m},\cdots,w_{c+m}|w_{c})}\\&=-\log{\prod_{j=0,j\ne m}^{2m}}\mathbb{P}(w_{c-m+j}|w_{c})\\&=-\log{\prod_{j=0,j\ne m}^{2m}\mathbb{P}(u_{c-m+j}|v_{c})}\\&=-\log{\prod_{j=0,j\ne m}^{2m}\frac{exp(u_{c-m+j}^{\top}v_{c})}{\sum_{k=1}^{|V|}exp(v_{k}^{\top}v_{c})}}\\&=-\sum_{j=0,j\ne m}^{2m}u_{c-m+j}^{\top}v_{c}+2m\log{\sum_{k=1}^{|V|}exp(u_{k}^{\top}v_{c})}\end{align*}$$ CBOW와 비교하여 주어진 center word에 대한 contexts들은 서로 독립이라는 가정이 추가된 것이 다르고, 위 목적함수를 기울기강하방법과 negative sampling, hierarchical softmax를 적용하여 학습하는 것은 같습니다. 

Skip-Gram 예시

마지막으로 "The boy is going to school."의 'The'를 context size 2, Skip-Gram으로 학습하는 프레임워크를 확인하고 정리하겠습니다.

Figure 4: Skip-Gram 예시

CBOW v.s. Skip-Gram

현재는 Skip-Gram을 CBOW보다 더 많이 이용하고 있습니다. 조금만 생각해보면 Skip-Gram이 왜 상대적으로 우세한지 알 수 있습니다. 계속 사용한 문장인 "The boy is going to school."을 이용하여 살펴보겠습니다.

Figure 5: CBOW v.s. Skip-Gram

가중치는 output과 가중치에 곱해져 나온 결과를 비교 평가하며 학습됩니다. 즉 빈번하게 학습될 수록 가중치가 적절히 평가될 가능성이 높습니다. Skip-Gram은 구조상 context로써 word가 CBOW와 비교하여 빈번하게 학습됩니다. 따라서 Skip-Gram이 대부분의 상황에서 더 좋은 성능을 보인다고 알려져있습니다.

마치며

이번 포스팅에서는 Word2vec에 대해서 살펴보았습니다. 다음 포스팅에서는 Negative sampling과 Hierarchical Softmax 방법에 대해서 포스팅을 하고 Glove라는 word embedding 방법도 글을 올릴예정입니다. 감사합니다. :)

References

• https://web.stanford.edu/class/cs224n/ 
• Mikolov, Tomas, et al. "Efficient estimation of word representations in vector space." arXiv preprint arXiv:1301.3781(2013).
• Bengio, Yoshua, et al. "A neural probabilistic language model." Journal of machine learning research 3.Feb (2003): 1137-1155.
• Mikolov, Tomáš, et al. "Recurrent neural network based language model." Eleventh annual conference of the international speech communication association. 2010.