Word2vec 학습

개요

이전 포스팅에서 Word2vec에 대해서 다루었습니다. CBOW와 Skip-Gram 모두 학습할 목적함수의 계산 복잡도가 높았습니다. CBOW의 목적함수는 $$\mathcal{L}_{CBOW}=-u_{c}^{\top}\hat{v}+\log{\sum_{j=1}^{|V|}exp(u_{j}^{\top}\hat{v})}$$와 같으며, Skip-Gram의 경우 $$\mathcal{L}_{skip-gram}=-\sum_{j=0,j\ne m}^{2m}u_{c-m+j}^{\top}v_{c}+2m\log{\sum_{k=1}^{|V|}exp(u_{k}^{\top}v_{c})}$$였습니다. 계산 복잡도가 높다는 말은 $|V|$와 직접적인 관련이 있습니다. $|V|$는 분석하고자하는 데이터로 부터 구축한 사전의 단어의 총 개수이고, 때문에 계산 복잡도는 $O(|V|)$가 됩니다. 이는 단어의 수가 많아지면 계산 복잡도가 선형으로 증가함을 의미합니다. 이런 계산 복잡도를 줄이기 위한 테크닉으로 negative sampling과 hierarchical softmax 방법이 고안되었습니다.  위 두 가지 방법은 단순히 학습 단계의 목적함수를 대체하기 위한 테크닉입니다. (개인적으로 처음 공부할 때 이 부분을 자꾸 놓쳐서 이해하는데 힘들었습니다. ㅠㅠ) 

Figure 1: Negative Sampling, Hierarchical Softmax가 적용되는 부분

Hierachical Softmax

개요

Hierarchical softmax는 출력층 값을 softmax 함수로 얻는 것 대신 binary tree를 이용하여 값을 얻는 방법입니다. Binary tree의 leaf은 각 단어와 대응되며, root 노드에서 각 leaf까지 unique path가 있고, 각 path는 확률과 대응됩니다. 각 노드에서 두 갈래의 path로 나누어지며 합이 1이 되도록 구성합니다. Hierarchical softmax는 root에서 부터 leaf까지 가는길에 있는 확률을 모두 곱하여 출력층의 값을 계산하게됩니다.

이해를 돕기 위해 "I have a car."라는 문장을 분석하는 상황을 고려해보겠습니다. 위 예제에서의 word는 'I', 'have', 'a', 'car', $|V|=4$가 됩니다. 이를 binary tree로 나타내면 아래 그림과 같습니다.

Figure 2: Binary tree, probability and unique path

이제 $|V|$를 일반화하여 hierarchical softmax를 이해해보겠습니다.

Notation

Figure 3: Binary tree

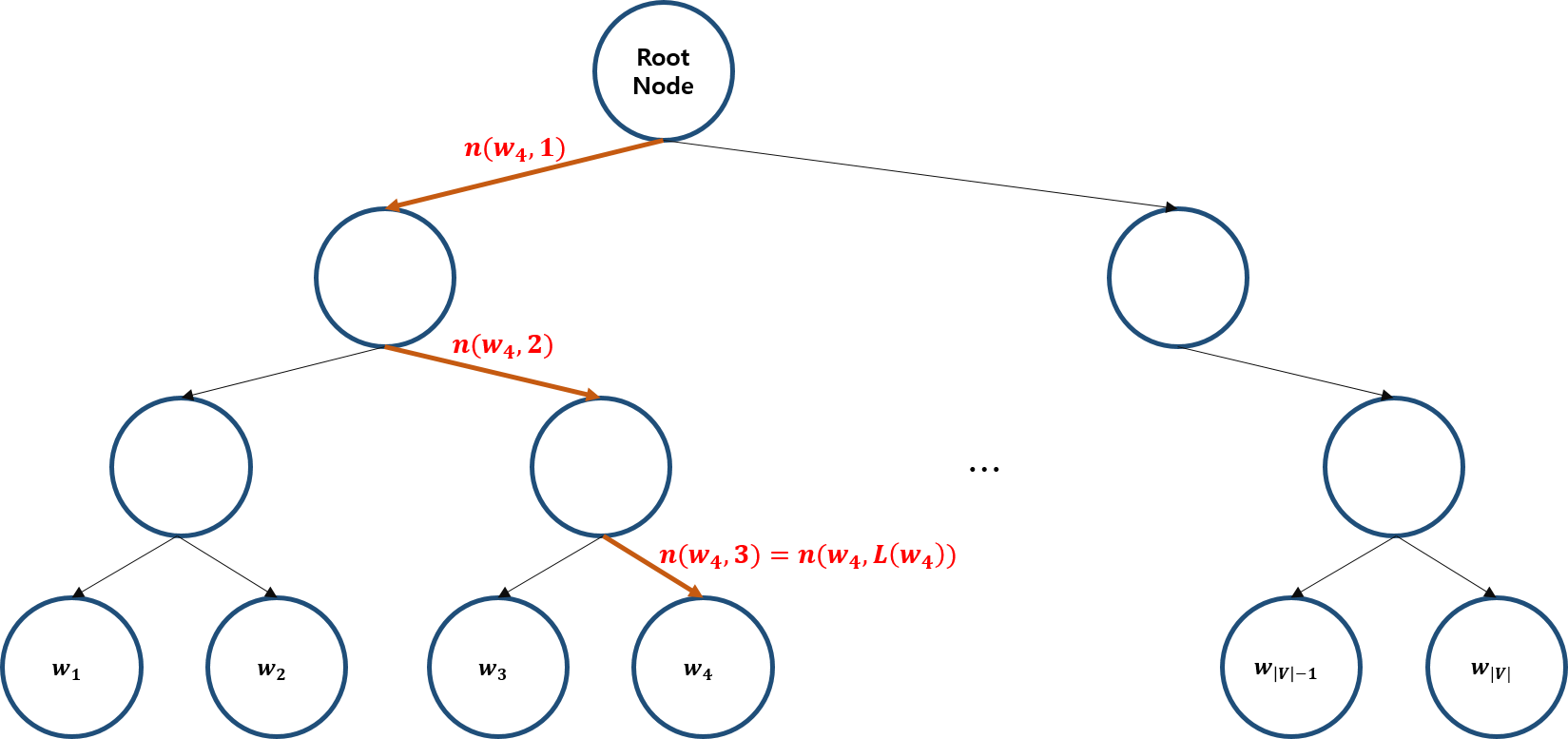
• $L(w)$: leaf 까지의 chlidren node의 수
• $n(w, i)$: $w$의 leaf 까지가는 $i$ 번째 chlidren node
  • $n(w, 1)$: root node
  • $n(w, L(w))$: leaf
• $ch\left(n(w,i)\right)$: $n(w,i)$의 자식 노드 중 한 쪽 (예를 들어, 항상 왼쪽 노드)
• $[[x]]$: $x$가 참이면 1, 거짓이면 -1
• $\sigma(x)=1/(1+e^{-x})$: sigmoid function
  • $\sigma(x)+\sigma(-x)=1$

Hierarchical softmax

입력 word $w_{I}$에 대한, 출력 word $w$의 hierarchical softmax는 아래와 같이 정의됩니다. $$\mathbb{P}(w|w_{I})=\prod_{j=1}^{L(w)-1}\sigma\left([[n(w,j+1)=ch\left(n(w,j)\right)]]\cdot v_{w_{I}}^{\top}v'_{n(w,j)})\right)$$

조금 자세히 살펴보도록 하겠습니다. 

첫 번째로 $n(w,j+1)=ch\left(n(w,j)\right)$의 의미를 살펴보겠습니다. 위에서 $ch\left(n(w,i)\right)$는 $n(w,i)$의 자식 노드 중 하나를 취하면 된다고 했고, 우리는 모든 노드에 대해서 왼쪽 노드를 가정하겠습니다. 그러면 $ch\left(n(w,j)\right)$는 이분된 것 중 좌측 노드를 뜻합니다. 즉 $n(w,j+1)$가 좌측에 있는 노드이면 1을 아니면, -1이 됩니다. 이렇게 하면 $\sigma(x)+\sigma(-x)=1$인 sigmoid function의 특성과 함께, 앞서 언급한 이분된 확률 합이 1이 되어야 된다는 가정을 항상 만족합니다. 

두 번째는 $v_{w_{I}}$와 $v'_{n(w,j)}$에 대한 이야기입니다. Softmax를 이용할 땐, input one-hot vector에 $\mathcal{V}$를 곱해, CBOW의 경우 $\hat{v}=\frac{\mathcal{V}x^{(c-m)}+\cdots+\mathcal{V}x^{(c+m)}}{2m}$을, Skip-gram은 $v_{c}=\mathcal{V}x$를 얻었습니다. 그리고 여기에 $\mathcal{U}$를 곱하고 $z=\mathcal{U}\hat{v}$ (CBOW) 그리고 $z=\mathcal{U}v_{c}$ (Skip-gram)을 얻어 $z$에 softmax을 취했습니다. 이제 다시 hierarchical softmax로 돌아오면 $v_{w_{I}}$는 $\hat{v}$와 $v_{c}$에 대응되고, output word matrix인 $\mathcal{U}$ 대신 binary tree의 모든 노드에 대응 되도록 $v'_{n(w,j)}$ 값을 이용하는 것입니다. 즉 $\mathcal{U}$를 학습하는 것 대신 $v'_{n(w,j)}$를 학습하는 것 입니다.

마지막으로 hierarchical softmax는 $\sum_{w=1}^{|V|}\mathbb{P}(w|w_{I})$을 만족합니다. 때문에 $|V|$개를 모두 계산하는 것보다 계산량이 줄면서, 합이 1이 되는 출력층을 계산할 수 있습니다.

마지막으로 Figure 3에 있는 $w_{4}$를 어떻게 계산하는지 살펴보고, hierarchical softmax를 마무리 하겠습니다. $$\begin{align*}\mathbb{P}(w_{4}|w_{i})&=\mathbb{P}\left(n(w_{4},1),L\right)\mathbb{P}\left(n(w_{4},2),R\right)\mathbb{P}\left(n(w_{4},3),R\right)\\&=\sigma\left(v_{w_{i}}^{\top}v'_{n(w_{4},1)}\right)\sigma\left(-v_{w_{i}}^{\top}v'_{n(w_{4},2)}\right)\sigma\left(-v_{w_{i}}^{\top}v'_{n(w_{4},3)}\right)\end{align*}$$

Negative Sampling

$|V|$개의 단어가 너무 많아서 계산이 힘들면 이 중 몇 개를 뽑아서 목적함수를 근사하는 방법을 생각해 볼 수 있습니다. Negative Sampling은 단어에 대한 어떤 노이즈 분포 $P_{n}(\omega)$를 가정하고, 분석 대상이된 corpus 외에 가정한 분포로 부터 random sampling with probability 방식으로 학습할 단어 몇 개를 추출하여 목적함수를 근사하는 방법입니다. 여기에서 $P_{n}(\omega)$는 단어 등장 빈도를 순서대로 정렬한 분포입니다.

Word와 context의 짝, $(\omega, c)$를 고려하겠습니다. $\mathbb{P}(D=1|\omega,c)$는 $(\omega,c)$가 corpus data에 있을 확률이고, 반대로 $\mathbb{P}(D=0|\omega,c)$는 corpus data에 없을 확률로 정의하겠습니다. 먼저 corpus에 있을 확률은 $$\mathbb{P}(D=1|w,c,\theta)=\sigma(v_{c}^{\top}v_{\omega})=\frac{1}{1+e^{-v_{c}^{\top}v_{w}}}$$로 sigmoid 함수와 함께 나타낼 수 있습니다.

Negative Sampling은 단어 몇 개를 sampling해서 entire word를 근사하는 것이 목적이기 때문에 새롭게 objective function을 정의해주어야 합니다. 새 목적함수를 정의하는 데 있어 핵심은 corpus에 등장하는 것과 아닌 것을 구분지어 likelihood를 정의해주는 것입니다. 먼저 $\theta$를 $\mathcal{U}$, $\mathcal{V}$에 등장하는 학습할 가중치라고 하면 likelihood는 다음과 같이 정의할 수 있습니다. $$\begin{align*}\theta&=\underset{\theta}{\operatorname{argmax}}\prod_{(\omega,c)\in D}\mathbb{P}(D=1|\omega,c,\theta)\prod_{(\omega,c)\in \bar{D}}\mathbb{P}(D=0|\omega,c,\theta)\\&=\underset{\theta}{\operatorname{argmax}}\prod_{(\omega,c)\in D}\mathbb{P}(D=1|\omega,c,\theta)\prod_{(\omega,c)\in\bar{D}}\left(1-\mathbb{P}(D=1|\omega,c,\theta)\right)\\&\propto \underset{\theta}{\operatorname{argmax}}\sum_{(\omega,c)\in D}\log{\mathbb{P}(D=1|\omega,c,\theta)}+\sum_{(\omega,c)\in\bar{D}}\log{\left(1-\mathbb{P}(D=1|\omega,c,\theta)\right)}\\&=\underset{\theta}{\operatorname{argmax}}\sum_{(\omega,c)\in D}\log{\frac{1}{1+e^{-u_{\omega}^{\top}v_{c}}}}+\sum_{(\omega,c)\in \bar{D}}\log{\frac{1}{1+e^{u_{w}^{\top}v_{c}}}}.\end{align*}$$ $\prod_{(\omega, c)\in\bar{D}}\mathbb{P}(D=0|\omega, c)$의 의미는 corpus에 등장하지 않는, ($D=0$), 단어들을 $\bar{D}$에서 추출하여 학습한다는 의미입니다. 이때 추출할 개수 $K$는 분석가가 정해주면 됩니다. Mikolov et al.에 따르면 데이터가 작을 경우 5~25 사이에서, 클경우 2~5 사이의 값을 선택하는 것이 실험결과가 좋다고 합니다. 이렇듯 negative sampling은 corpus에 등장하지 않는 단어를 위에서 말한 노이즈 분포 $P_{n}(\omega)$에서 얻어 학습하는 것입니다. 노이즈 분포 $P_{n}(\omega)$ 역시 분석가가 정해줄 수 있습니다. Mikolov et al.에 따르면 unigram model의 $3/4$ power를 적용한 것이 실험결과가 가장좋다고 합니다. $f$를 unigram model이라고 하면, 논문에서 제안한 노이즈 분포는 아래와 같습니다. $$P(\omega_{i})_{n}=\left(\frac{f(\omega_{i})}{\sum_{j=1}^{n}f(\omega_{j})}\right)^{3/4}$$

결국 위 log-likelihood를 최대화 한다는 것은 negative log-likelihood를 최소화 하는 것과 같으므로, 목적함수를 다음과 같이 정의할 수 있습니다. $$J=-\sum_{(\omega,c)\in D}\log{\frac{1}{1+e^{-u_{\omega}^{\top}v_{c}}}}-\sum_{(\omega,c)\in\bar{D}}\log{\frac{1}{1+e^{u_{\omega}^{\top}v_{c}}}}$$ 위 내용을 $K$개 negative sampling 하는 CBOW와 Skip-gram에 다시 적용하면, 각각 아래처럼 나타낼 수 있습니다. $$J_{CBOW}=-\log{\sigma(u_{c}^{\top}\hat{v})}-\sum_{k=1}^{K}\log{\sigma(-u_{k}^{\top}\hat{v})}$$ $$J_{Skip-gram}=-\log{\sigma(u_{c}^{\top}v_{c})}-\sum_{k=1}^{K}\log{\sigma(-u_{k}^{\top}v_{c})}$$

Subsampling Frequent Words

Negative sampling과 유사한 방법으로 subsamping frequent words라는 방법이 있습니다. Subsampling은 특정 단어 몇 개를 분석에서 제외하는 점이, 매 iteration마다 몇 개의 단어만 학습하는 negative sampling과 구분되어집니다.

많은 corpus가 존재할 경우 "in", "the", "a"와 같은 단어들은 상대적으로 많이 등장하여 자주 학습될 것입니다. 하지만 역설적으론 드물게 등장하는 단어에 비해 정보가 적음을 의미합니다. Subsampling frequent words는 이렇게 의미없게 많이 등장하는 단어를 분석에서 제외하는 방법으로 아래 분포 기반 단어를 분석에서 제외합니다. $$\mathbb{P}(\omega_{i})=1-\sqrt{\frac{t}{f(\omega_{i})}}$$ 여기에서 $t$는 분석가가 정해주는 값으로 $t$가 클수록 더욱 공격적으로 단어들을 분석에서 제외합니다. Mikolov et al.에 따르면 $t$는 $10^{-5}$ 전후를 권장하고 있습니다.

References

• https://web.stanford.edu/class/cs224n/
• Mikolov, Tomas, et al. "Distributed representations of words and phrases and their compositionality." Advances in neural information processing systems. 2013.