기울기 강하법 기본

본 포스팅에서는 답러닝 역전파 알고리즘에 적용되는 여러 기울기 강하법을 익히기 위한 기본 개념에 대해서 정리하려고 합니다. 초보적인 내용부터, Batch Gradient Descent, Stochastic Gradient Descent, Mini-Batch Gradient Descent까지 살펴보겠습니다.

기울기 강하법 (Gradient Descent Algorithms)

인공신경망의 가중치를 학습하기 위해서 기울기 강하법을 사용합니다. 기울기 강하법은 국소 최소값(Local Minimum)을 찾기 위한 수치적인 방법(numerical method)으로 기울기의 역방향으로 값을 조금씩 움직여 함수의 출력 값이 수렴할 때까지 반복하는 방법입니다

어떤 함수 $f$의 국소 최소값을 찾기 위한 기울기 강하법은 $$x^{(k+1)}\leftarrow x^{(k)}-\gamma_{k}\frac{\partial f(x^{(k)})}{\partial x^{(k)}}$$입니다. 여기서 $\gamma_{k}$는 learning rate 혹은 step-size라고 불리우는데 기울기의 역방향으로 $x$를 이동할 크기를 조정하는 역할을 합니다.

기울기 강하법에서 주의해야 할 두가지가 있습니다. 첫 번째는 초기값 $x^{(0)}$이며, 두 번째는 learning rate $\gamma_{k}$입니다. 만약 learning rate가 적절하지 못하면 다음의 문제가 발생합니다.

Figure 1: Learning Rate와 Gradient Descent

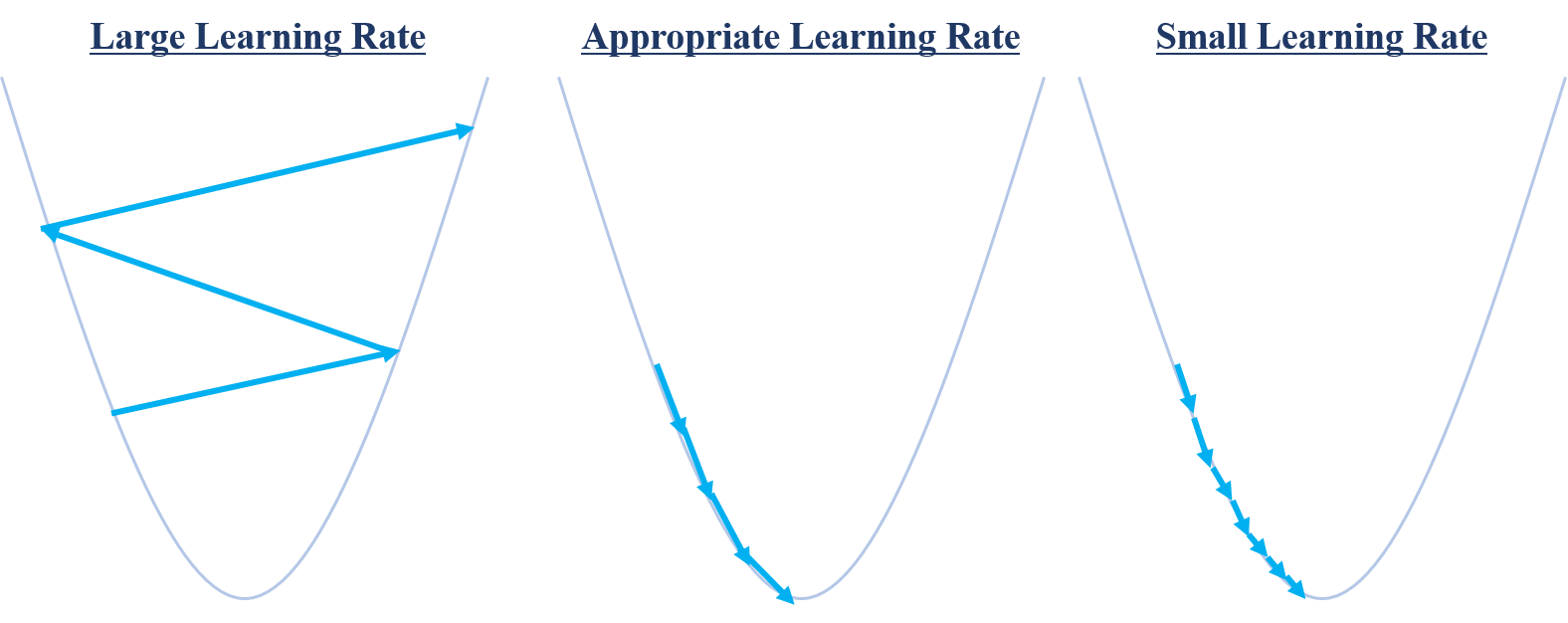
최소값을 찾기 위해 움직이는데 학습률이 너무 크면 오히려 알고리즘이 수렴하지 않고 발산해버릴 수도 있습니다. 만약 값이 너무 작다면 수렴까지 오랜시간이 걸리게 됩니다. 가운데 상황처럼 적당한 학습률을 정해줄 필요가 있습니다. 만약 함수가 울퉁불퉁하다면 즉 convex또는 concave 함수가 아니라면 초기값에 따라 국소 최소값이 달라지게 됩니다.

Figure 2: Initial Value와 Gradient Descent

Figure 2처럼 같은 learning rate를 이용했을 경우 어디서 출발하느냐에 따라서 국소 최소값의 결과가 달라질 수 있습니다.

기울기 강하법 예제 1

$f(x)=x^{2}$의 최소값을 찾기 위한 기울기 강하법 예제를 살펴보겠습니다. 기울기는 $\frac{\partial f}{\partial x}=2x$로 얻어집니다. 최소값을 찾기 위한 기울기 강하법은 $$x \leftarrow x - \gamma\times2x$$로 적용할 수 있습니다.

Figure 3: 기울기 강하법 예제

학습률 0.2, 0.4에 대하여 각각 기울기 강하법을 적용한 결과로 각각 10, -10에서 시작했습니다. 단순한 convex 함수기 때문에 학습률이 클수록 빠르게 수렴하는 것을 확인 할 수 있습니다.

기울기 강하법 예제 2

4차 함수 $f(x)=x^{4}+x^{3}-3x^{2}-x+2$의 최소값을 찾기 위한 기울기 강하법 예제를 살펴보겠습니다. 기울기는 $\frac{\partial f}{\partial x}=4x^{3}+3x^{2}-6x-1$로 얻어집니다. 최소값을 찾기 위한 기울기 강하법은 $$x \leftarrow x - \gamma\times \left(4x^{3}+3x^{2}-6x-1\right)$$로 적용할 수 있습니다.

Figure 4: 기울기 강하법 예제

학습률 0.01, 0.1에 대하여 각각 기울기 강하법을 적용한 결과로 모두 2에서 시작했습니다. 같은 지점에서 시작했지만 학습률이 0.01인 경우 이동크기가 너무 작아 국소 최소값이 빠진 것을 확인 할 수 있습니다. 반면 학습률을 0.1인 경우 국소 최소값을 빠져나와 전체 최소값으로 수렴한 것을 확인 할 수 있습니다.

기울기 강하법 예제 3

절편이 없는 회귀직선 $y=0.7x+\epsilon$, $\epsilon\sim N(0,1)$을 고려하겠습니다. 다시 말해서  $y=\beta x$의 $\beta$를 기울기 강하법으로 추정해보겠습니다. 즉 MSE 손실함수 $$\sum_{i=1}^{N}\left(y-\beta x\right)^{2}$$를 최적화하는 방법입니다. 최적화의 대상인 $\beta$의 기울기는 $$-\sum_{i=1}^{N}x(y-\beta x)$$가 되며, 기울기 강하법의 학습률 0.02를 적용한 update rule은$$\beta\leftarrow\beta+0.02\sum_{i=1}^{N}x(y-\beta x)$$가 됩니다. 회귀직선의 관점에서 살펴보면 Figure 5와 같습니다.

Figure 5: 기울기 강하법 회귀 분석 적용 예제

이어서 손실함수 관점에서는

Figure 6: 기울기 강하법 회귀 분석 손실함수 관점

예제 3은 결국 입력변수 1개, 은닉층 0개, 출력함수  identity, 손실함수 MSE인 인공 신경망과 같습니다.

---

데이터 크기에 따른 기울기 강하법 (Gradient Descent Algorithms by Amount of Data)

예제 1, 2는 단순히 이해를 돕기 위한 것이 었다면, 예제 3은 데이터 기반 가중치 학습을 했다는 점이 큰 차이입니다. Figure 5의 점들이 데이터인데, 예제 3에서는 전체 데이터에 대한 MSE Loss를 계산하고, 가중치를 여러번 update하면서 최적 가중치를 찾았습니다. 눈치 채셨겠지만 update를 진행할 때 데이터를 일부만 사용하더라도 충분히 update가 가능합니다.

Update에 이용되는 데이터의 크기에 따라서 Batch Gradient Descent, Mini-Batch Gradient Descent, Stochastic Gradient Descent로 구분합니다. 이때 데이터 전부를 사용하는 것을 1 에폭 (Epoch)이라고 합니다. 예를 들어, 데이터의 크기가 $N$일 때, $N$개의 데이터를 이용해서 가중치를 업데이트 하는 것은 $1 update = 1 epoch$이 되고, $10$개의 데이터를 이용하면 $1 update = \frac{1}{N} epoch$이 됩니다. 

Batch Gradient Descent

데이터 전체를 사용해서 가중치를 update하는 방법입니다. 즉 예제 3번이 정확히 Batch Graident Descent 입니다.

for i in range(epochs):
	prams.grad = evaluate.gradient(loss, data, parameters)
    prameters  = prameters - learning.rate * prams.grad

Mini-Batch Graident Descent

데이터의 일부를 랜덤하게 추출해서 가중치를 update하는 방법입니다.

for i in range(epochs):
	random.shuffle(data)
    for batch in get.batchs(data, batch.size):
    	params.grad = evaluate.gradient(loss, batch, parameters)
        parameters  = parameters - learning.rate * params.grad

Stochastic Graident Descent

데이터 1개를 랜덤하게 추출해서 가중치를 update하는 방법입니다.

for i in range(epochs):
	random.shuffle(data)
    for example in data:
    	prams.grad = evaluate.gradient(loss, example, parameters)
        parameters = parameters - learning.rate * params.grad

 

크기 $N$의 데이터를 고려하여, 요약하면 Mini-Batch Gradient Descent의 데이터 추출크기가 $m$이라고 했을 때, $m=N$이면 Batch Gradient Descent와, 이어서 $m=1$이면 Stochastic Gradient Descent와 같습니다.

---

마치며

인공신경망의 역전파 방법은 Stochastic Gradient Descent 기반 발전했습니다. 위에서 살펴 보았듯 기울기 강하법은 초기값 설정과 학습률에 크게 영향받습니다. 이 문제를 해결하기 위한 여러 방법과 컴퓨터 성능의 발전으로 인공신경망이 크게 발전했는데, 다음 포스팅에서 다뤄질 초기값 설정과 학습률을 처리하는 여러 방법의 등장과 함께 Deep Learning이라는 이름으로 바뀌어 불리기 시작했습니다.

---

References

• Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016).