본 내용은 "An overview of gradient descent optimization algorithms."을 참고하여 작성하였습니다.
기울기 강하법 기본 포스팅에서 기울기 강하법의 기초적인 내용과 강하법시 이용되는 데이터의 크기에 따라서 Batch, Mini-Batch, Stochastic Gradient Descent를 구분했습니다. 위 세 가지 알고리즘을 편의상 앞에 "Vanilla(기본의)"를 붙여부르도록 하겠습니다.
용어의 혼란을 줄이기 위해 첨언하면, 통상적으로 딥러닝 프레임워크(tensorflow, keras 등)에 적용된 Batch Gradient라는 컨셉은 Mini-batch를 의미합니다.
Challenges
Vanilla Mini-batch Gradient Descent는 좋은 수렴이 보장되진 않습니다. 하지만 다음의 상황을 생각해보면 어느정도 감을 잡을 수 있습니다.
- 적절한 학습률(Learning Rate)을 선택하는 것이 어렵습니다.
- 그래서 적절한 학습률을 선택하기 위해, 알고리즘 초반에는 과감히 움직이고, 학습이 거듭될 수록 학습률을 감소시키도록 학습률 스케쥴링(Learning Rate Schedules)을 합니다. 하지만 미리 스캐쥴을 잡아야되는 것과 데이터의 특성에 따라 그때 그때 정해줘야되는 번거로움이 있습니다.
- 두 번째 방법의 또 다른 단점은 모든 가중치에 대해서 똑같은 학습률이 적용된다는 점입니다. 만일 학습이 빨리 끝난 가중치가 존재한다면 해당 가중치의 학습률을 크게 줄이는 것이 합리적일 것입니다.
- 이전 포스팅에서 살펴 보았듯 심각한 non-convex 함수에 대해서는 local minima에 빠질 위험이 커집니다. 즉 안장점(Saddle Points)에 빠질 수 있습니다. 만약 안장점일 경우 좀 더 힘껏 기울기의 역방향으로 이동한다면 빠져나올 수 있을 것입니다.
위에서 다룬 네 가지 힌트를 mini-batch gradient descent에 잘 녹여낸 방법들을 이어서 다루겠습니다.
Momentum
SGD를 사용할 경우 같은 학습률을 이용하기 때문에 골짜기에 빠 질 확률이 큽니다. 달리 말해서 울퉁불퉁한 함수에서 국소 최소값에 도달할 확률이 크다는 말이 됩니다.

Momentum 방법은 SGD이 가고자 하는 방향에 가속을 주는 방법입니다. 위 그림을 보면 모멘텀을 주었을때 골짜기를 빠르게 벗어나는 것을 볼 수 있습니다. $$\begin{align*}v_{t}&=\gamma v_{t-1}+\eta \nabla_{\theta}J(\theta)\\\theta&=\theta-v_{t}\end{align*}$$ 보통 $\gamma=0.9$ 또는 작은 값으로 설정합니다. (정해진 값이 아니라 해당 모멘텀의 크기가 학습이 잘 된다고 알려져 있습니다.) 이를 도식화하면 figure 2와 같습니다.

모멘텀을 직관적으로 이해하기 위해 내리막길을 굴러가는 공을 상상해보면, 공은 같은 방향으로 굴러 내려갈 수 록 속도가 빨라 질 것이 자명합니다. 달리 말해서 모멘텀은 기울기의 역방향에 이전의 크기를 만큼 더 해줌으로써 골짜기를 박차고 나올 힘이 생기게 됩니다.
Nesterov Accelerated Gradient
올바른 길을 가기 위해서 공이 단순히 내리막 길을 점점 빨리 내려가기만 하는 것 보다는 적당한 지점부터 속도를 늦춰야 안정적으로 도착할 수 있습니다. 상기 내용을 반영한 것이 Nesterov Accelerated Gradient (NAG) 방법입니다.
NAG는 가중치($\theta$)에 모멘텀이 반영된 기울기 만큼 이동($\gamma v_{t-1}$)했을 때, 이동분 $\theta-\gamma v_{t-1}$만큼을 반영해 주는 방법입니다. 즉 현재 위치에서의 기울기가 아닌 미래 위치(근사치)의 기울기를 반영한 방법입니다. $$\begin{align*}v_{t}&=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta-\gamma v_{t-1})\\\theta&=\theta-v_{t}\end{align*}$$ 모멘텀 방법과 마찬가지로 $\gamma=0.9$로 설정해주는 것이 좋다고 알려져 있습니다. 이를 모멘텀 방법과 비교하여 도식화하면 다음과 같습니다.

Figure 3의 주황색이 파란색과 구분되는 점은 $t$이 아닌 $t-1$시점에서의 기울기를 이용하여 미리 이동한 지점에서의 기울기를 이용하는 점입니다. Nesterov 방법을 Momentum과 비교하여 보면 상대적으로 느린 속도로 값이 update된다는 점을 알 수 있고, Nesterov는 너무 빠르게 기울기가 수정되는 것을 방지할 수 있습니다. Nesterov는 RNN 모형의 학습 성능을 의미있게 발전시켰다고 알려져있습니다.
Adagrad (ADAptive subGRADients)
Momentum과 NAG는 모든 가중치에 동일한 학습률 $\eta$를 적용해 왔습니다. 하지만 직관적으로 생각해보면 어떤 가중치는 빠르게 학습이 끝날 수 도 있고, 다른 경우에서는 더 큰 학습률 적용이 필요한 경우도 있을 것 입니다. 이렇듯 빈번히 업데이트가 일어나는 가중치의 학습률은 작게하고, 반대의 경우는 크게하는 방법을 고안했고, data가 sparse한 경우 학습이 잘 된다고 알려져있습니다. (예를 들어, word embedding의 GloVe)
먼저 각 가중치에 대한 기울기를 $$g_{t,i}=\nabla_{\theta_{t}}J(\theta_{t,i})$$로 정의하겠습니다. 이어서 SGD를 각 가중치에 대해 나타내면 $$\theta_{t+1,i}=\theta_{t,i}-\eta g_{t,i}$$로 나타낼 수 있습니다. Adagrad는 SGD의 학습률을 조정해주는 방법으로 다음과 같이 정의됩니다. $$\theta_{t+1,i}=\theta_{t,i}-\frac{\eta}{\sqrt{G_{t,ii}+\epsilon}}\cdot g_{t,i},$$ 여기에서 $G_{t}\in\mathbb{R}^{d\times d}$는 대각 행렬이며, 그 원소로는 $t$ 시점까지의 $\theta_{i}$의 기울기의 제곱합이고, $\epsilon$은 분모가 0이 되는 걸 방지하기 위한 아주 작은 상수로 일반적으로 $1e-8$을 적용합니다. 이제 elementwise matrix vector 곱 연산자인 $\odot$을 이용하여 Adagrad를 정리하면, $$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{G_{t}+\epsilon}}\odot g_{t}$$로 나타낼 수 있습니다.
눈치채셨겠지만 Adagrad 방법은 학습시간이 길어지면 분모가 과도하게 커져 학습률이 0으로 수렴할 수 있는 문제점을 가지고 있습니다. 이를 보완한 방법이 이어질 Adadelta 방법이 되겠습니다.
Adadelta
Adadelta에서는 Adagrad의 분모가 과도하게 커지는 것을 방지하기 위하여, 무작정 더하지 않고, gradient의 가중평균을 구해줍니다. 즉, $$\mathbb{E}[g^{2}]_{t}=\gamma\mathbb{E}[g^{2}]_{t-1}+(1-\gamma)g_{t}^{2}.$$ 조금만 더 풀어 써보겠습니다. $$\begin{align*}\mathbb{E}[g^{2}]_{t}&=\gamma\left[\gamma\mathbb{E}[g^{2}]_{t-2}+(1-\gamma)g_{t-1}^{2}\right]+(1-\gamma)g_{t}^{2}\\&=\gamma^{2}\mathbb{E}[g^{2}]_{t-2}+(1-\gamma)\left[\gamma g_{t-1}^{2}+g_{t}^{2}\right]\end{align*}$$ 보시다시피 연속적으로 가중평균을 취해주는 것은 과거의 gradient를 지수적으로 감소 (exponentially decay) 시킵니다. 요약하여 Adadelta는 Adagrad의 분모가 과도하게 작아지는 것을 방지하기 위해 시점 $t$에서의 기울기 변화를 크게 반영하고 과거의 것은 적게 반영 시킵니다.
vanilla SGD는 $$\begin{align*}\Delta\theta_{t}&=-\eta g_{t,i}\\\theta_{t+1}&=\theta_{t}+\Delta\theta_{t}\end{align*}$$로 나타낼 수 있고, Adagrad는 $\Delta\theta_{t}$를 $$\Delta\theta_{t}=-\frac{\eta}{\sqrt{G_{t}+\epsilon}}\odot g_{t}$$로 나타 낼 수 있습니다.
지금부터 Adadelta로 확장하겠습니다. Adagrad의 분모에 위 가중평균을 적용하면, $$\Delta\theta_{t}=-\frac{\eta}{\sqrt{\mathbb{E}[g^{2}]_{t}+\epsilon}}g_{t}=-\frac{\eta}{RMS[g]_{t}}g_{t},$$ 여기에서 $RMS$는 단순히 root mean squared 함수 입니다. Adadelta를 제안한 논문을 살펴보면 앞선 SGD, Momentum, Adagrad 모두 가중치의 업데이트 단위(unit)이 일치하지않는 문제점이 있고, second order numerical 최적화 방법 (예를 들어, Newton의 방법)에 귀감을 받아 가중치 업데이트 단위를 맞추고자 가중치 업데이트 변화량에 대한 가중평균 한 가지를 더 정의합니다. $$\mathbb{E}[\Delta\theta^{2}]_{t}=\gamma\mathbb{E}[\Delta\theta^{2}]_{t-1}+(1-\gamma)\Delta\theta^{2}_{t}=\sqrt{\mathbb{E}[\Delta\theta^{2}]_{t}+\epsilon}=RMS[\Delta\theta]_{t}$$ 이어서 글로벌 학습률인 $\eta$를 $RMS[\Delta\theta]_{t}$로 대체합니다.
요약하여 Adadelta 알고리즘을 나타내면, $$\begin{align*}\Delta\theta_{t}&=-\frac{RMS[\Delta\theta]_{t-1}}{RMS[g]_{t}}g_{t}\\\theta_{t+1}&=\theta_{t}+\Delta_{t}\end{align*}$$로 정리할 수 있습니다.
RMSprop
RMSprop는 publish된 논문이 따로 있지 않고, Geoff Hinton Coursera강좌의 강의자료에 제안된 내용입니다. RMSprop는 Adadelta에서 업데이트 단위를 맞춰주는 작업 이전까지의 방법입니다. $$\begin{align*}\mathbb{E}[g^{2}]_{t}&=\gamma\mathbb{E}[g^{2}]_{t-1}+(1-\gamma)g_{t}^{2}\\\theta_{t+1}&=\theta_{t}-\frac{\eta}{\sqrt{\mathbb{E}[g^{2}]_{t}+\epsilon}}g_{t}\end{align*}$$ Hinton은 decay rate $\gamma$를 0.9로 제안했고, 글로벌 학습률 $\eta$를 0.001로 제안했습니다.
Adam
Adam은 ADaptive Moment Estimation의 줄인말로 각 가중치에 학습률을 다르게 주는 또다른 방법입니다. Adam은 Adadelta처럼 학습과정 중 발생한 gradient의 제곱을 지수적으로 감소하는 가중 평균을 적용하는 것 말고도, gradient 그 자체를 지수적으로 감소하는 가중 평균을 적용하여 학습률에 반영합니다. $$\begin{align*}m_{t}&=\beta_{1}m_{t-1}+(1-\beta_{1})g_{t}\\v_{t}&=\beta_{2}v_{t-1}+(1-\beta_{2})g_{t}^{2}\end{align*}$$ 위 가중평균 $m_{t}$, $v_{t}$는 불편 추정량(unbiased estimator)이 아닙니다.
불편 추정량이 아닌 것을 보이기 위해 몇 가지 가정을 하겠습니다. $g_{1},\cdots,g_{T}$는 시간 순서대로 발생한 step $t$에서의 gradients이고, $g_{t}\sim p(g_{t})$입니다. 또한 우리는 $v_{0}=0$, $m_{0}=0$으로 초기화 하여 알고리즘을 진행합니다. 그러면 $m_{t}$는 $m_{t}=(1-\beta_{1})=\sum_{i=1}^{t}\beta_{1}^{t-i}g_{i}$로 나타낼 수 있습니다. 이어서 양변에 기대값을 취해주면, $$\begin{align*}\mathbb{E}[m_{t}]&=\mathbb{E}\left[(1-\beta_{1})\sum_{i=1}^{t}\beta_{1}^{t-i}g_{i}\right]\\&=\mathbb{E}[g_{t}](1-\beta_{1})\sum_{i=1}^{t}\beta_{1}^{t-i}+\zeta\\&=\mathbb{E}[g_{t}](1-\beta_{1}^{t})+\zeta\end{align*}$$로 나타낼 수 있습니다. 여기에서 만약 $\mathbb{E}[g_{i}]$가 stationary하면 $\zeta=0$이 되며, 아닌 경우 아주 작은 수가 됩니다. 위 사실로 부터 $1-\beta_{1}^{t}$로 나누어 주어야 불편추정량이 된다는 것을 알 수 있습니다. $v_{t}$도 같은 방법으로 유도할 수 있고, 정리하면 $$\hat{m}_{t}=\frac{m_{t}}{1-\beta_{1}^{t}}, \hat{v}_{t}=\frac{v_{t}}{1-\beta_{2}^{t}}$$가 됩니다.
Adam의 알고리즘은 1) $g_{t}$를 계산하여 2) $m_{t}$, $v_{t}$를 얻고, 다시 3) $\hat{m}_{t}$, $\hat{v}_{t}$를 계산한 것을 이용하여 다음의 update rule을 가중치에 적용합니다. $$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}+\epsilon}}\hat{m}_{t}$$ 마지막으로 Adam의 저자는 기본값으로 $\beta_{1}=0.9$, $\beta_{2}=0.999$, $\epsilon=10^{-8}$을 제안했습니다.
AdaMax
AdaMax는 Adam 논문에 같이 수록되어 있는 방법입니다. Adam의 update 룰의 단위(scale)는 $v_{t}$는 $t$ step 이전의 gradients의$l_{2}$ norm 역수와 $t$ step의 gradient $|g_{t}|^{2}$에 비례하여 증가 합니다. $l_{2}$ norm에 대한 내용을 $l_{p}$ norm으로 확장시킬 수 있습니다. 먼저 $\beta_{2}$는 $$v_{t}=\beta_{2}^{p}v_{t-1}+(1-\beta_{2}^{p})|g_{t}|^{2}$$로 나타낼 수 있습니다. 이때 $p\rightarrow\infty$로 보내면, $$\begin{align*}u_{t}=\lim_{p\rightarrow\infty}(v_{t})^{1/p}&=\lim_{p\rightarrow\infty}\left((1-\beta_{2}^{p})\sum_{i=1}^{t}\beta_{2}^{p(t-i)}|g_{i}|^{p}\right)^{1/p}\\&=\lim_{p\rightarrow\infty}(1-\beta_{2}^{p})^{1/p}\left(\sum_{i=1}^{t}\beta_{2}^{p(t-i)}|g_{i}|^{p}\right)^{1/p}\\&=\lim_{p\rightarrow\infty}\left(\sum_{i=1}^{t}\left(\beta_{2}^{(t-i)}|g_{i}|\right)^{p}\right)^{1/p}\\&=\max{\left(\beta_{2}^{t-1}|g_{1}|,\cdots,\beta_{2}|g_{t-1}|,|g_{t}|\right)}\end{align*}$$가 됩니다. 결국엔 반복적(recursively)으로 알고리즘을 수행하기 때문에 $$u_{t}=\max{(\beta_{2}u_{t-1},|g_{t}|)}$$가 되고 초기값은 $u_{0}=0$으로 시작합니다. 결국엔 $l_{2}$ norm에서 $l_{\infty}$ norm으로 확장시켰기 때문에 AdaMax라는 이름이 붙었으며 $p=2$보다 $p=\infty$에서 좀더 안정적으로 값이 수렴한다고 합니다.
AdaMax 알고리즘은 1) $g_{t}$를 계산하여, 2) $m_{t}$, $v_{t}$, $\hat{m}_{t}$(Adam과 동일)를 순차적으로 얻고, 이를 이용하여 다음의 update룰을 가중치에 적용합니다. $$\theta_{t+1}=\theta_{t}-\frac{\eta}{u_{t}}\hat{m}_{t}$$
정리하며
논문에는 Adam에 Nesterov를 적용한 Nadam까지 수록되어 있습니다. 아래 Ruder, Sebastian. "An overview of gradient descent optimization algorithms."에서 찾아 볼 수 있습니다.
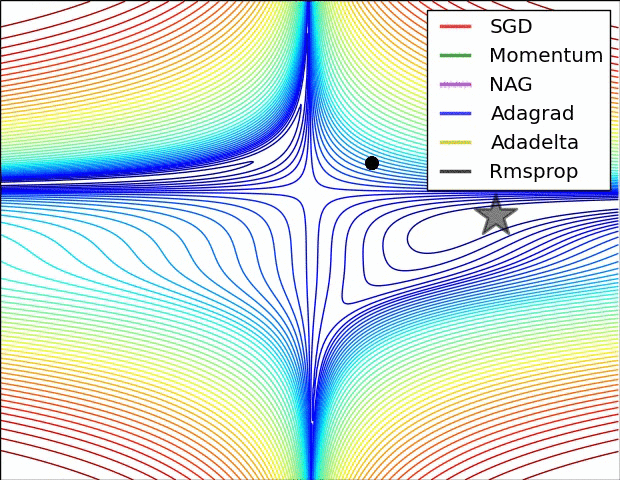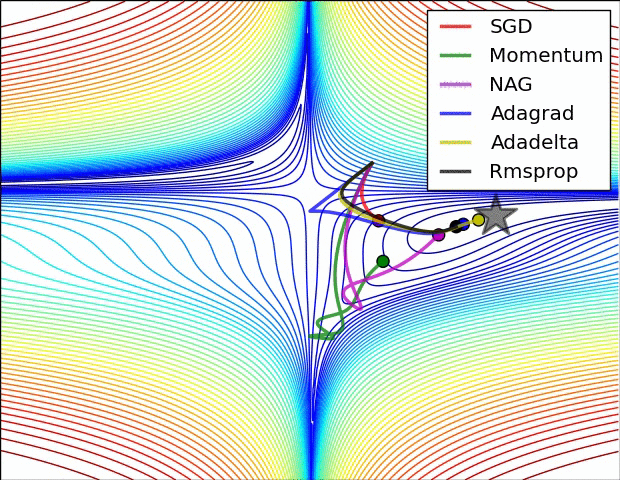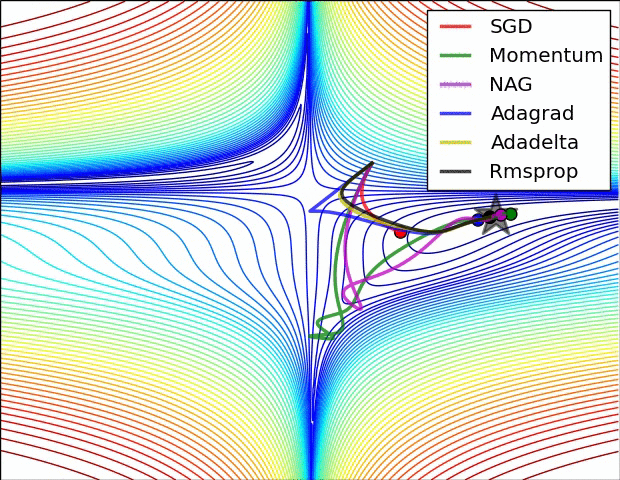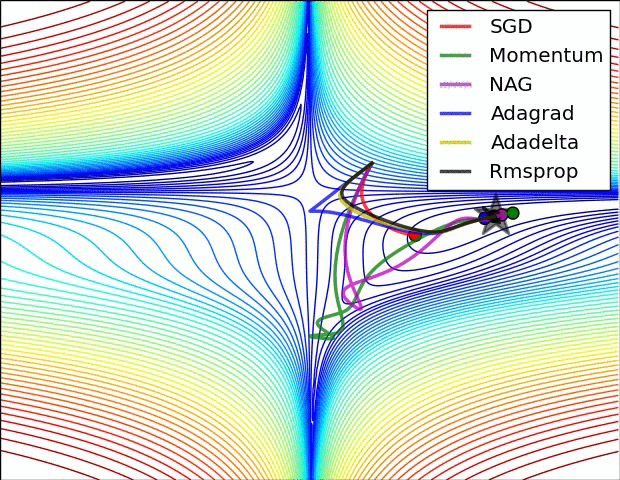

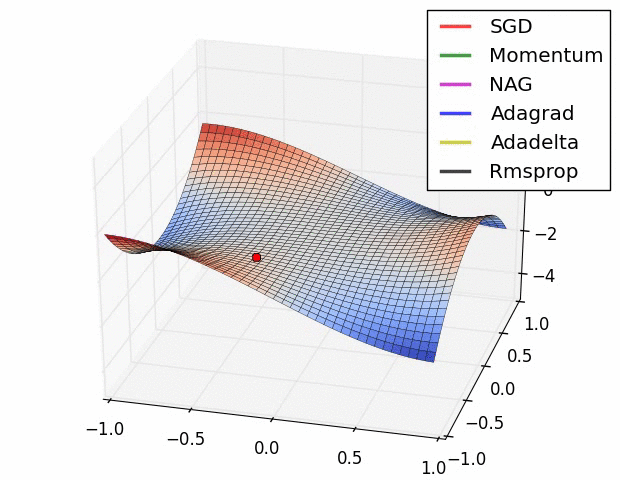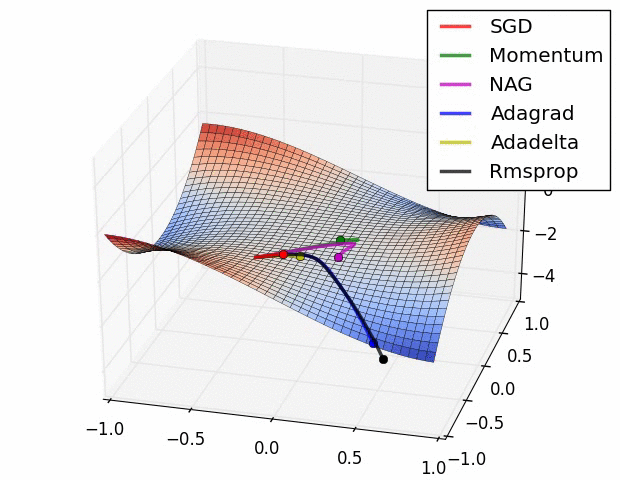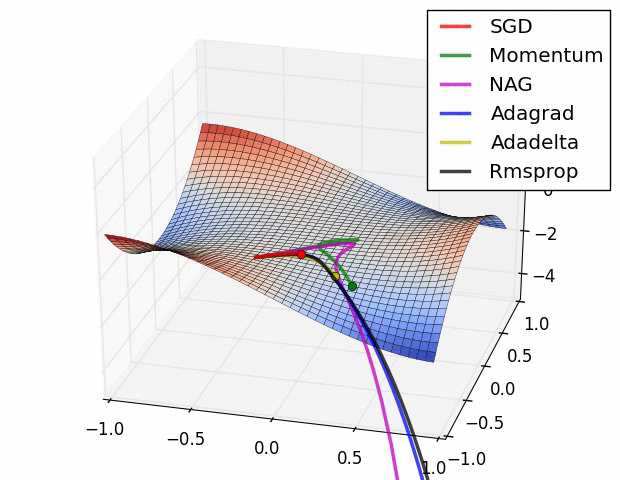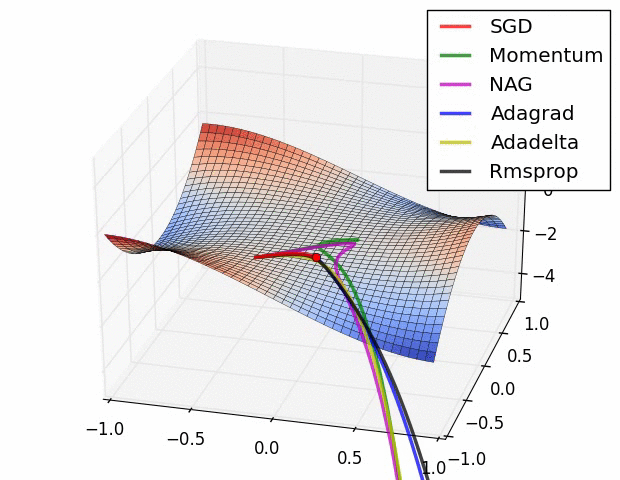
참고 논문에 등장하는 방법의 수렴 속도에 대한 비교입니다. 사실 눈치채셨겠지만 어떤 방법이 절대적으로 좋다는 건 없습니다. 데이터의 형태, 적용되는 딥러닝 프레임워크에 따라서 전부 다르기 때문에 실제 분석시에는 경험적인 노력이 필요합니다.
References
- Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016).
- Kingma, Diederik P., and Jimmy Ba. "Adam: A method for stochastic optimization." arXiv preprint arXiv:1412.6980 (2014).
- Zeiler, Matthew D. "ADADELTA: an adaptive learning rate method." arXiv preprint arXiv:1212.5701 (2012).
'Deep Learning > Optimization' 카테고리의 다른 글
| 기울기 강하법 기본 (0) | 2019.06.01 |
|---|
댓글