이번 포스팅에서는 저번 포스팅에서 살펴본 Value function과 Bellman Equation, 그리고 행동전략인 정책 (Policy)을 정의하여 MDP를 푸는 방법을 살펴보고 강화학습의 뼈대인 MDP를 마무리하도록 하겠습니다.
Policy
에이전트와 환경의 상호과정 속 에이전트는 상태를 확인하고 이에 맞는 행동을 합니다. 이렇게 에이전트가 특정 상태에서 어떤 행동을 할 것 인지를 확률로 정의하는 것을 정책(policy)이라고 합니다. (사실 확률이라는 용어를 사용했지만 선호도에 가깝긴합니다.) $$\text{policy}=\pi(a|s)$$ 정책을 확률로 정의하면서 우리는 앞에서 정의한 return의 기대값을 구할 수 있게 됩니다.
Bellman Equation
Bellman Equation은 이어서 정의할 가치함수 (Value Function)를 즉각보상과 뒤따르는 보상의 합으로 풀어서 쓴 식을 의미하며, 이를 풀면 최적의 의사결정을 할 수 있습니다. 가치함수와 Bellman Equation을 순서대로 살펴보겠습니다.
Value Function
가치함수는 에이전트가 놓인 상태 또는 상태와 행동 쌍의 가치를 함수로써 표현한 것입니다. 상태의 가치를 나타낸 함수를 상태가치함수 (State-Value Function), 상태와 행동의 쌍의 가치를 나타낸 것을 행동가치함수 (Action-Value Function)라고 부릅니다. 상태가치함수는 어떤 정책 $\pi$아래 $$\begin{align*}v_{\pi}(s)&=\mathbb{E}_{\pi}\left[G_{t}|S_{t}=s\right]\\&=\mathbb{E}_{\pi}\left[\left.\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\right| S_{t}=s\right]\\&=\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma G_{t+1}\right|S_{t}=s\right]\end{align*}$$로 정의됩니다. 여기에서 $G_{t}$는 누적보상인 return을 의미합니다. 제일 뒷단의 식을 보면 $R_{t+1}$과 $G_{t+1}$로 쪼개에 두었는데 이를 각각 즉각보상과 뒤따르는 보상으로 이해할 수 있습니다. 이어서 행동가치함수는 어떤 정책 $\pi$아래 $$\begin{align*}q_{\pi}(s, a)&=\mathbb{E}_{\pi}\left[G_{t}|S_{t}=s, A_{t}=a\right]\\&=\mathbb{E}_{\pi}\left[\left.\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\right| S_{t}=s, A_{t}=a\right]\\&=\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma G_{t+1}\right|S_{t}=s, A_{t}=a\right]\end{align*}$$로 정의됩니다.
Bellman Equation
가치함수를 벨만방정식으로 표현해보고 어떤 관계에 놓여있는지 살펴보겠습니다. 먼저 상태가치함수입니다. $$\begin{align*}v_{\pi}(s)&=\mathbb{E}_{\pi}\left[\left.G_{t}\right|S_{t}=s\right]\\&=\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma G_{t+1}\right|S_{t}=s\right]\\&=\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma\mathbb{E}_{\pi}[\left.G_{t+1}\right|S_{t+1}=s']\right|S_{t}=s\right]\\&=\sum_{a}\pi(a|s)\sum_{s',r}\mathbb{P}(s',r|s,a)\left[r+\gamma\mathbb{E}_{\pi}\left[\left.G_{t+1}\right|S_{t+1}=s'\right]\right]\\&=\sum_{a}\pi(a|s)\sum_{s',r}\mathbb{P}(s',r|s,a)\left[r+\gamma v_{\pi}(s')\right]\\&=\sum_{a}\pi(a|s)q_{\pi}(s,a)\end{align*}$$ 여기에서 제일 뒷단 두개의 식을 상태가치함수의 벨만방정식이라고 부릅니다. (제일 마지막식은 행동가치함수와 같이봐야 이해가 됩니다.)
이어서 행동가치함수의 벨만방정식을 유도해보겠습니다. $$\begin{align*}q_{\pi}(s,a)=&\mathbb{E}_{\pi}\left[\left.G_{t}\right|S_{t}=s, A_{t}=a\right]\\=&\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma\mathbb{E}_{\pi}(G_{t+1}|S_{t+1}=s')\right|S_{t}=s,A_{t}=a\right]\\&\text{ or }\mathbb{E}_{\pi}\left[\left.R_{t+1}+\gamma\mathbb{E}(G_{t+1}|S_{t+1}=s',A_{t+1}=a')\right|S_{t}=s,A_{t}=a\right]\\=&\mathbb{E}\left[\left.R_{t+1}+\gamma v_{\pi}(s')\right|S_{t}=s,A_{t}=a\right]\\&\text{ or }\mathbb{E}\left[\left.R_{t+1}+\gamma q_{\pi}(s',a')\right|S_{t}=s,A_{t}=a\right]\\=&\sum_{r,s'}\mathbb{P}(s',r|s,a)[r+\gamma v_{\pi}(s')]\\&\text{ or }\sum_{r,s',a'}\mathbb{P}(r,s',a'|s,a)[r+\gamma q_{\pi}(s',a')]\end{align*}$$ 마찬가지로 제일 뒷단의 식이 행동가치함수가 되는데, 상태가치함수가 내재된 형태와 행동가치함수가 내재된 형태 두 가지로 나타낼 수 있습니다.
상태가치함수, 행동가치함수의 벨만방정식을 back-up diagram을 이용해 이해해보겠습니다.
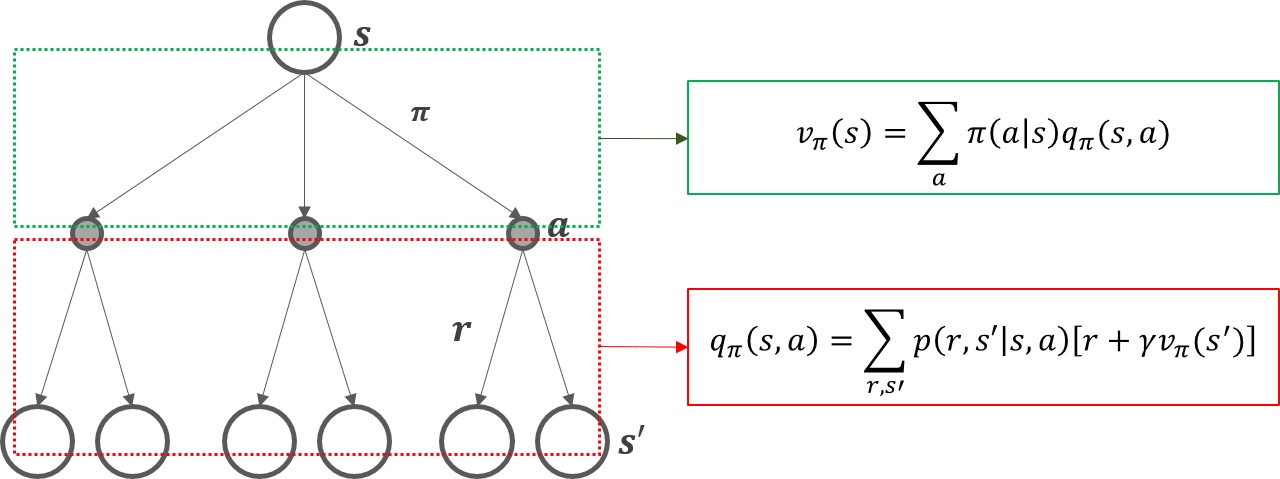
Back-up diagram이라고 불리우는 이유는 아래에서 위 방향으로 계산이 이루어져서 입니다. 상태가치함수 $v_{\pi}(s)$는 뒤따를 행동가치함수의 정책기반의 가중평균으로 이해할 수 있고, 행동가치함수 $q_{\pi}$는 다음 상태가치함수에 대한 보상과 상태전이확률의 결합확률의 가중평균으로 이해할 수 있습니다.
벨만 방정식을 풀면 각 상태와 행동의 가치를 판단할 수 있게됩니다. 이를 이용하여 MAB에서 다루었던 $\epsilon$-greedy 전략과 같은 방법을 적용하면 최적의 의사결정을 할 수 있습니다. 이어서 가치함수 기반 의사결정을 할때 어떤 정책이 가장 좋은 가치를 만들어내는지 살펴보겠습니다.
Bellman Optimality Equation
Optimal Policy
MDP 문제를 해결한다는 것은 장기적으로 큰 보상을 얻는 정책을 찾는다는 말과 어느정도 같은 말입니다. 그만큼 좋은 정책을 찾는 것은 중요합니다. 다행히도 어떤 MDP라도 적어도 1개 이상의 최적 정책이 존재합니다. 최적 정책의 정의는 다음과 같습니다. 최적정책을 $\pi_{*}$라고 하면 $$\pi_{*}\ge \pi \text{ if and only if } v_{\pi_{*}}(s)\ge v_{\pi}(s)\text{, }\forall s\in\mathcal{S}.$$ 위 상황을 만족하는 $\pi_{*}$를 모두가 최적 정책입니다. 모두라는 표현을 쓴 것은 여러개의 최적 정책이 존재할 수 있기 때문입니다.
Optimal Value Functions
최적 정책인 $\pi_{*}$들은 가치함수를 공유합니다. 즉 여러개의 최적 정책이 있다고 하더라도 가치함수는 동일하다는 말입니다. 어쨋든 최적 정책도 정책이기 때문에 최적 정책아래 가치함수를 정의 할 수 있는데 이를 최적가치함수(optimal value functions)라고 부릅니다. 또한 위에서 optimal policy 정의에 따라서 상태가치함수는 다음이 만족합니다. $$v_{*}(s)=\underset{\pi}{\operatorname{max}}v_{\pi}(s)\text{, }\forall s\in\mathcal{S}$$ 상태가치함수와 행동가치함수는 단순히 행동까지 결정된 상태에서 return의 기대값을 계산하는가의 차이만 존재합니다. 결국 return의 기대값을 구하는 것이기 때문에 직관적으로 최적행동가치함수는 최적상태가치함수의 값이 같음을 알 수 있습니다. 따라서 행동가치함수도 다음과 같이 표현 할 수 있습니다. $$q_{*}(s,a)=\underset{\pi}{\operatorname{max}}q_{\pi}(s,a)\text{, }\forall s\in\mathcal{S}\text{, }a\in\mathcal{A}(s).$$ 행동가치함수와 상태가치함수를 같이 아래와 같습니다. $$q_{*}(s,a)=\mathbb{E}\left[\left.R_{t+1}+\gamma v_{*}(S_{t+1})\right|S_{t}=s,A_{t}=a\right]$$
Bellman Optimality Equation
Bellman Optimality Equation은 Bellman Equation을 최적정책 $\pi_{*}$하에서 유도한 결과입니다. 최적상태가치함수와 최적행동가치함수 순으로 살펴보겠습니다. 위에서 말했다시피 최적상태가치함수와 최적행동가치함수의 결과는 같기 때문에 같은 상태에서 최대의 가치함수 값을 출력하는 행동가치함수의 행동을 선택하면 최적상태가치함수와 결과가 같게됩니다. $$\begin{align*}v_{*}(s)=&\underset{a\in\mathcal{A}(s)}{\operatorname{max}}q_{\pi_{*}}(s,a)\\=&\underset{a}{\operatorname{max}}\mathbb{E}_{\pi_{*}}\left[\left.R_{t+1}+\gamma G_{t+1}\right|S_{t}=s,A_{t}=a\right]\\=&\underset{a}{\operatorname{max}}\mathbb{E}_{\pi_{*}}\left[\left.R_{t+1}+\gamma v_{*}(S_{t+1})\right|S_{t}=s,A_{t}=a\right]\\=&\underset{a}{\operatorname{max}}\sum_{s',r}\mathbb{P}(s',r|s,a)\left[r+\gamma v_{*}(s')\right]\end{align*}$$ 마지막 두 개의 식이 최적행동벨만방정식이됩니다. 이어서 최적행동가치함수의 벨만방정식을 유도해보면, $$\begin{align*}q_{*}(s,a)=&\mathbb{E}\left[\left.R_{t+1}+\gamma v_{*}(S_{t+1})\right|S_{t}=s,A_{t}=a\right]\\=&\mathbb{E}\left[\left.R_{t+1}+\gamma\underset{a'}{\operatorname{max}}q_{*}(S_{t+1},a')\right|S_{t}=s,A_{t}=a\right]\\=&\sum_{s',r}\mathbb{P}(s',r|s,a)\left[r+\gamma\underset{a'}{\operatorname{max}}q_{*}(s',a')\right]\end{align*}$$ 위 식에서 마지막 두줄로 얻을 수 있습니다. Back-up diagram을 통해 조금 더 직관적으로 살펴보겠습니다.

Bellman Equation과 비교했을 때 Bellman Optimality Equation은 가중평균을 구하는 것이 아니라 최대값의 방향으로 행동하는 것이 차이점입니다. 최적상태가치함수는 뒤따를 행동가치함수중 최대가 되는 쪽으로 back-up diagram이 이동하고, 행동가치함수는 뒤따를 상태가치함수의 최대값에 대한 가중평균임을 알 수 있습니다.
MDP에선 Bellman Optimality Equation의 unique solution이 존재한다고 알려져있습니다. 또한 최적가치함수를 찾고 탐욕적(greedy)으로 행동을 선택하면 다행히도 장기적으로 큰 보상을 얻을 수 있음도 마찬가지 입니다. 하지만 예상가능컨데 상태공간의 크기가 거대해지면 계산 복잡도가 커지게 되어 한계에 봉착합니다.
마치며
이번 포스팅에서는 벨만방정식이 어떤 것 인지 알아봤고, 이전 포스팅과 함께 MDP의 전반적 내용을 다루었습니다. MAB와 MDP를 어느정도 이해하고 나면, 본격적으로 강화학습을 이해하는 기본기가 생깁니다. 결국 MDP를 정의한다는 것은 강화학습 문제를 정의하는 것과 동일선상에 있습니다. 그런데 MDP 포스팅에서 결론적으로 유일한 최적가치함수가 존재한다고 했지 어떻게 계산하는지는 내용이 없습니다. 이번 포스팅 말미에 다루었듯 상태공간의 크기, 행동공간의 크기 등에 따라 복잡한 문제의 경우 계산복잡도가 굉장히 큽니다. 그래서 가치함수를 계산하기 위해 간단한 문제의 경우는 tabular method를 이용하고, 복잡한 문제의 경우에는 approximate method를 적용합니다. 크게 이 두 가지 틀안에서 강화학습의 방법들을 익힐 수 있습니다. 이어질 포스팅에서는 강화학습 학습 방법론으로 찾아뵙겠습니다. 감사합니다:)
References
- Sutton, Richard S., and Andrew G. Barto. Introduction to reinforcement learning. Vol. 2. No. 4. Cambridge: MIT press, 1998.
'Reinforcement Learning > Introduction' 카테고리의 다른 글
| Markov Decision Process (1) - 개요 (0) | 2019.10.02 |
|---|---|
| Multi-Armed Bandit for RL(3) - Gradient Bandit Algorithms (0) | 2019.09.17 |
| Multi-Armed Bandit for RL(2) - Action Value Methods (0) | 2019.09.15 |
| Multi Armed Bandit for RL(1) - 개요 (2) | 2019.09.15 |
| 강화학습개요 (0) | 2019.09.12 |



댓글