이번 포스팅에서는 강화학습의 골격을 잡아주는 Markov Decision Process (MDP)의 개요에 대해 알아보겠습니다. MDP의 가치함수 정의 및 최적 정책결정에 대해서는 다음 포스팅에서 자세히 다루겠습니다.
MDP는 순차적 의사결정 (sequential decision process)을 하기 위한 아주 고전적인 방법론입니다. 이전 포스팅에서 살펴보았듯 강화학습은 에이전트가 환경과 상호작용을 하며 보상을 최대화하는 방향으로 학습합니다. 이렇게 상호작용의 과정을 순차적으로 나타낼 수 있기 때문에 강화학습문제를 MDP로 정의 할 수 있습니다. 강화학습은 문제를 MDP로 정의하는 것으로 출발하기 때문에 MDP는 강화학습 전반에 걸쳐서 중추적인 역할을 합니다.
Agent-Environment Interface
MDP를 살펴보기 앞서 에이전트와 환경의 상호작용을 살펴보겠습니다.

에이전트와 환경을 정의하면, 에이전트는 학습의 주체, 의사 결정자, 행동의 주체이며, 환경은 에이전트를 제외한 모든 것입니다. 에이전트는 $S_{t}$라는 상태에서 $A_{t}$라는 행동을 하면 환경이 이를 관측하고, $R_{t+1}$의 보상과 다음 상태 $S_{t+1}$을 에이전트에 전달합니다. 이를 간단하게 요약하면, $$S_{0}, A_{0}, R_{1}, S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, R_{3}, S_{3}, \cdots$$으로 나타 낼 수 있는데, 이를 sequence 또는 trajectory라고 부릅니다.
Markov Decision Process (MDP)
Markov Property를 갖는 전이확률을 이용하여 의사결정하는 것을 MDP라고 합니다. 먼저 Markov Property란 $t$ 시점에 어떤 사건이 발생할 확률은 오직 $t-1$시점에만 영향을 받는 성질을 말합니다. 이를 수식으로 나타내면 다음과 같습니다. $$\mathbb{P}(X_{t}|X_{t-1})=\mathbb{P}(X_{t}|X_{t-1},X_{t-2},\cdots)$$ MDP를 정의하기 위해 몇가지 구성요소로 $\mathcal{S}$, $\mathcal{A}$, $\mathcal{R}$ 각각 상태, 행동, 보상의 집합이 필요합니다. 에이전트와 환경의 상호작용을 MDP로 이해할 수 있고, 상태, 행동, 보상을 확률로 $$\mathbb{P}(s',r|s,a)=\mathbb{P}(S_{t}=s', R_{t}=r|S_{t-1}=s, A_{t-1}=a)$$ 정의할 수 있고, 상태전이확률(state-transition probability)이라고 부릅니다. 상태전이확률을 model이라고 부르고 상태전이확률을 알때 적용 가능한 방법을 model-based methods라고 부르며, 모르는 경우에도 적용할 수 있는 방법을 model-free-methods라고 부릅니다. 여기에서 $s,s'\in\mathcal{S}$, $r\in\mathcal{R}$, $a\in\mathcal{A}(s)$가 되겠습니다. 상태전이확률은 $S_{t-1}=s$ 상태에서 $A_{t-1}=a$를 했을 때, $R_{t}=r$의 보상을 얻고, 다음 상태 $S_{t}=s'$에 놓여 있을 확률입니다. 하나 첨언을 하면 markov property를 가정했기 때문에 $$\mathbb{P}(S_{t},R_{t}|S_{t-1},A_{t-1})=\mathbb{P}(S_{t},R_{t}|S_{t-1},A_{t-1},S_{t-2},A_{t-2},\cdots)$$가 성립합니다.
상태전이확률을 예제와 함께 이해해보겠습니다. 아래는 $2\times 2$ 크기의 미로찾기문제입니다. 에이전트는 시작지점에서 출발하여 도착지점까지 도달하면됩니다. 이 미로는 좌, 우, 아래, 위 방향으로만 이동가능합니다. 즉, $\mathcal{A}=\{\leftarrow, \rightarrow, \downarrow, \uparrow\}$라는 말과 동일합니다. 또한 도착지점에 도달할 경우는 1의 보상을 받고, 함정 칸에서 출발지점으로 돌아가면 보상이 -2, 이를 제외한 나머지 모든 움직임에서는 보상이 -1입니다. 달리 말하면, $\mathcal{R}=\{-2,-1,1\}$인 것 입니다. 마지막으로 각 네모는 상태를 말합니다. 마찬가지로 요약해보면 $\mathcal{S}=\{(1,1),(1,2),(2,1),(2,2)\}$ 에이전트는 낭떠러지가 있음을 자각한다고 가정하겠습니다. (예를 들어 (1,1) 지점에서는 위, 오른쪽 방향으로만 이동가능합니다.)
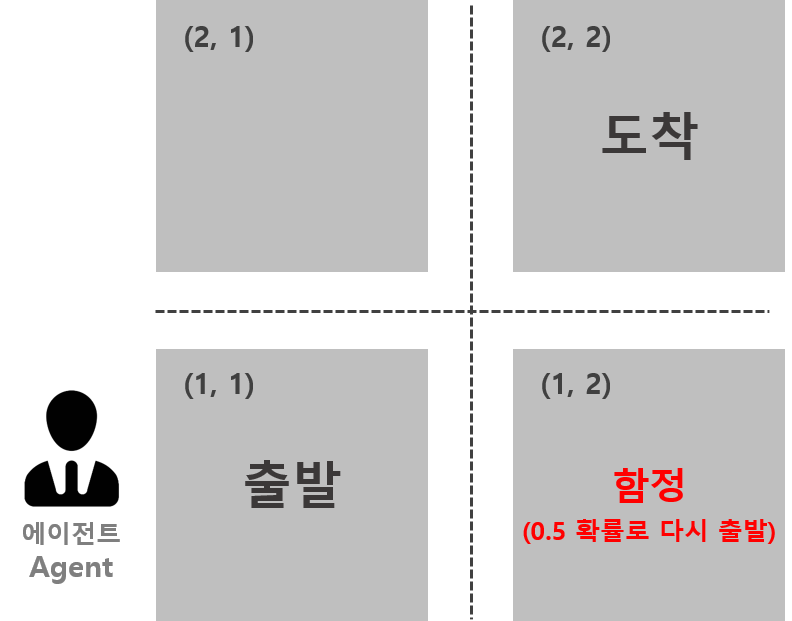
상태전이확률 몇 가지를 나태내면 아래와 같습니다. $$\begin{align*}0.5&=\mathbb{P}\left((1,2), -1|(1,1),\rightarrow\right)\\0.5&=\mathbb{P}\left((1,1),-2|(1,1), \rightarrow\right)\\1&=\mathbb{P}\left((2,1),-1|(1,1),\uparrow\right)\end{align*}$$ 여기서 한 가지 짚고 넘어갈 것은 같은 상태에서 같은 행동을 하더라도, 결과가 확률적으로 다를 수 있다는 점 입니다.
Goals for Markov Decision Process
MDP의 목적은 아주 간단합니다. 에이전트가 환경과 끊임없이 상호작용하며 얻는 '누적'보상이 최대가 되도록 순차적으로 의사결정하는 것입니다. 즉, 현재 상태에서 다음 상태로 전환될 때 얻는 보상을 최대화하는 것이 아니라 장기적인 관점의 보상을 최대화한다는 의미입니다. 따라서 우리가 순차적의사결정 문제를 MDP로 정의할 때 보상은 큰 틀에서 정해주는 것이 좋습니다. 예를 들어 넘어진 로봇이 일어서서 걷는 문제를 MDP로 접근할 경우 보상은 걷는 경우에 집중하여 정하는 편이 낫습니다. 만약에 로봇이 일어나는 부분에 보상을 집중시키면 로봇이 직립은 하지만 걷는 방법은 터득하지 못 할 가능성이 크기 때문입니다.
Return & Episode
앞서 MDP의 목적은 누적보상을 최대화하는 것이라고 했습니다. 우리는 앞으로 누적보상을 고상한 말로 Return이라고 부릅니다. $$G_{t}=R_{t+1}+R_{t+2}+\cdots+R_{T}$$ 위와 같이 $t$ 시점에서의 Return은 $t+1$ 시점의 보상부터 종료 상태인 $T$ 시점까지의 보상의 합으로 정의할 수 있습니다. 이렇게 상태가 $t=1$에서 시작해서 $t=T$로 끝나는, 즉 한 sequence의 단위를 우리는 episode라고 부릅니다.
눈치 채셨겠지만 어떤 MDP 문제에서 $T$는 존재할 수도, 안 할 수도 있습니다. 달리 말하면 종료상태가 있는 문제가 있고, 끝이 없는 문제가 있습니다. $T$가 유한하냐 ($T<\infty$) 혹은 무한하냐 ($T=\infty$)에 따라서 각각 episodic task, continuing task로 분류됩니다.
자연스럽게 Return은 단순합이기 때문에 continuing task에서는 무한대의 값을 갖게됩니다. Episodic task 또한 종료 시점인 $T$가 엄청 큰 경우에는 Return이 너무 먼 미래의 정보를 담고있어 학습이 더딜 수 있습니다. 그래서 미래의 보상을 할인(discount)해서 return을 정의할 수 있고, 이를 discounted return이라고 부릅니다. $$\begin{align*}G_{t}&=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\cdots\\&=R_{t+1}+\gamma G_{t+1}\end{align*}$$ 여기에서 $\gamma\in[0, 1]$이며, $\gamma$를 할인율 (discounted rate)이라고 부릅니다. 할인율은 0에서 1사이 값을 갖기 때문에 시간이 충분히 지나고 나면 0에 수렴하기 때문에 discounted return은 항상 유한하다는 사실을 알 수 있습니다. 할인율은 0에 가까울수록 현재지향적이고 1에 가까울수록 미래지향적입니다.
마치며
이번 포스팅에서는 MDP의 기본적인 내용에 대해서 다루었습니다. MDP를 정의하고 난다음에는 의사결정위한 수치적인 기준이 필요한데, 이를 가치함수라고 부릅니다. 따라서 다음 포스팅에서 상태가치함수 및 행동가치함수라는 것을 정의해야하니 다음 포스팅에서 자세히 다루도록 하겠습니다. 감사합니다 :)
References
- Sutton, Richard S., and Andrew G. Barto. Introduction to reinforcement learning. Vol. 2. No. 4. Cambridge: MIT press, 1998.
'Reinforcement Learning > Introduction' 카테고리의 다른 글
| Markov Decision Process (2) - Bellman Equation (2) | 2019.10.03 |
|---|---|
| Multi-Armed Bandit for RL(3) - Gradient Bandit Algorithms (0) | 2019.09.17 |
| Multi-Armed Bandit for RL(2) - Action Value Methods (0) | 2019.09.15 |
| Multi Armed Bandit for RL(1) - 개요 (2) | 2019.09.15 |
| 강화학습개요 (0) | 2019.09.12 |



댓글