이번 포스팅에서는 CNN의 가중치를 학습하기 위한 역전파가 계산이 어떻게 이루어지는지 살펴 보겠습니다.
이번 포스팅에서 이미지 픽셀 좌표는 좌상단에서 0 부터 시작하기로 약속하겠습니다.

예를 들어 3x3 이미지에서는 (0, 0)으로 시작해서 (2, 2)로 끝나는 형태입니다. 역전파를 하려면 그래디언트가 필요합니다. Convolutional layer의 연산을 수식으로 표현해보겠습니다. 보통 CNN 구조는 Convolutional Layer, Activation Function, Pooling의 순으로 분석이 진행됩니다. 이를 도식화 하면 다음과 같습니다.
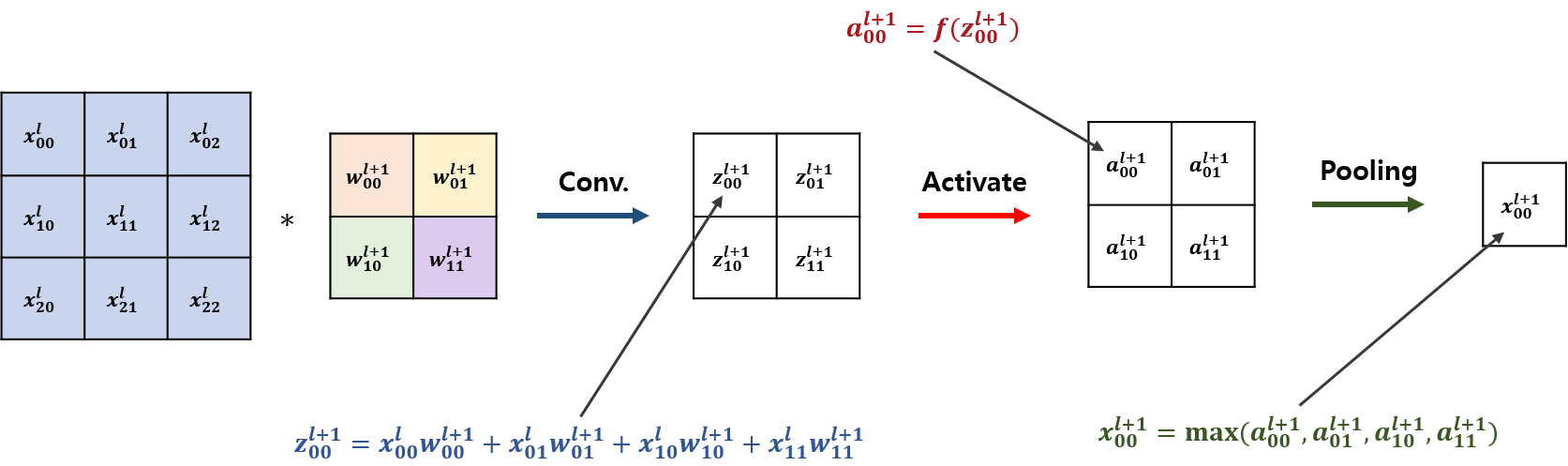
큰 흐름은 입력($x$)에 필터 가중치($w$)로 convolution하고($z$), 이를 활성화 시킨 뒤($a$), Pooling($x$)하는 절차입니다. (가중치 윗 첨자 $(l+1)$은 $l$ 레이어에서 $(l+1)$ 레이어로 가는 가중치라는 의미로 본 포스팅에서 통일하겠습니다.) 먼저 convolution 부분을 살펴보겠습니다. $z_{00}^{l+1}$은 입력값 (0, 0), (0, 1), (1, 0), (1, 1)과 필터 (0, 0), (0, 1), (1, 0), (1, 1)에 대응하는 점에 대해 곱을 한 후 이를 합한 결과로 나머지 값도 같습니다. 다음 활성함수 $f$를 이용하여 해당 값을 활성화합니다. 본 포스팅에서는 활성함수는 계산 편의 및 가장 널리 이용되는 ReLu를 고려하겠습니다. 마지막으로 활성화 된 Pooling을 가정하고 활성화된 값 중 가장 큰 값을 출력합니다.
이제 위 내용을 일반적인 상황으로 확장해 보겠습니다. $$z_{ab}^{l+1}=\sum_{m=0}^{m_{l+1}-1}\sum_{n=0}^{n_{l+1}-1}w_{mn}^{l+1}x_{a+m,b+n}^{l}$$ $$a_{ab}^{l+1}=f\left(z_{ab}^{l+1}\right)$$ $$x_{ij}^{l+1}=\underset{i\times j\in\{2i,2i+1,\cdots\ 2i+m_{l+1}\}\times\{2j,2j+1,\cdots,2j+n_{l+1}\} }{\operatorname{max}}z_{ij}^{l+1}$$ 여기에서 convolution 스트라이드는 1, pooling의 스트라이드는 2를 가정했습니다. 여기에서 표기법은 다음과 같습니다.
- $a\in\{0,\cdots,(a^{l}-1)\}$, $b\in\{0,\cdots,(b^{l}-1)\}$로 Convolution 및 Activation 직후의 데이터의 가로($a$), 세로($b$) 위치입니다.
- $i\in\{0,\cdots,(i^{l}-1)\}$, $j\in\{0,\cdots,(j^{l}-1)\}$ Pooling 이후의 데이터의 가로($i$), 세로($j$) 위치입니다.
- $l$은 레이어의 번호로 $l\in\{1,\cdots,L\}$이 되며, $L$은 출력층 직전의 레이어입니다.
이번 포스팅은 아주 간단한 예제로 CNN의 Backpropagation을 이해해보려고합니다. Figure 2에 도식화된것이 전체 CNN 구조라고 생각하고 끝에다 출력층만 붙여보겠습니다.

상단의 그림은 Figure 2에서 출력층을 덧붙인 것이고, 하단의 그림은 같은 상황을 인공신경망으로 나타낸 것 입니다. 가중치를 공유하는 것과 local connectivity를 강조하기 위해, 앞단의 화살표에 색을 칠해 두었습니다. 이제 입력값($x_{00}^{l},\cdots,x_{22}^{l}$)과 실제값 ($y_{1}$)에 대해 Backpropagation을 계산해보겠습니다. 출력값 $o_{1}$과 실제값 $y_{1}$에 대한 손실함수를 $L$이라고 하겠습니다. (계산상 편의를 위해 손실함수를 특정하지 않고 진행하고, $f$, $g$ 모두 ReLu를 가정하겠습니다.)
학습대상 가중치들은 filter의 가중치 4개($w_{00}^{l+1},\cdots,w_{11}^{l+1}$)와 pooling 결과와 출력층 연결 가중치 1개($w_{0}^{l+2}$)가 됩니다. 출력층 가중치에 대한 기울기를 구해보면, $$\frac{\partial L}{\partial w_{0}^{l+2}}=\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial w_{0}^{l+2}}=\frac{\partial L}{\partial o_{1}}x_{00}^{l+1}$$ 가 됩니다. 다음 가중치는 Max-pooling 연산 가중치가 됩니다. Max-pooling의 경우 $a_{00}^{l+1},\cdots,a_{11}^{l+1}$중 가장 큰 값에 대해서 항등함수(identity)의 결과를 출력합니다. 즉 4개의 가중치 중 단 1개가 기울기 1로 존재하며, 나머지에 대해선 기울기가 0이 됩니다. 그러면 $(a',b')$을 활성화 값의 최대값의 위치라고 하겠습니다. 그러면, $$\frac{\partial L}{\partial pool_{a',b'}}=\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial pool_{a',b'}}=\frac{\partial L}{\partial o_{1}}w_{0}^{l+2}$$로 얻을 수 있습니다. 이제 filter의 가중치를 살펴보겠습니다. $w_{00}^{l+1}$을 Figure 3과 함께 살펴보면, 다음 레이어의 모든 값에 영향을 주었다는 것을 알 수 있습니다. 다만 $x_{00}^{l}$, $x_{01}^{l}$, $x_{10}^{l}$, $x_{11}^{l}$에 대하여 영향을 줍니다. 이에 따라 $w_{00}^{l+1}$의 기울기는 $$\frac{\partial L}{\partial w_{00}^{l+1}}=\sum_{a=0}^{a^{l+1}-1}\sum_{b=0}^{b^{l+1}-1}\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial a_{ab}^{l+1}}\frac{\partial a_{ab}^{l+1}}{\partial w_{00}^{l+1}}$$이 되며, 나머지 3개도 다를게 없기에 $$\frac{\partial L}{\partial w_{ij}^{l+1}}=\sum_{a=0}^{a^{l+1}-1}\sum_{b=0}^{b^{l+1}-1}\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial a_{ab}^{l+1}}\frac{\partial a_{ab}^{l+1}}{\partial w_{ij}^{l+1}}$$가 된다는 사실을 알 수 있습니다. (여기에서 $i\in\left\{0, \cdots, (m_{l+1}-1)\right\}$, $j\in\left\{0, \cdots, (n_{l+1}-1)\right\}$) $\frac{x_{00}^{l+1}}{a_{ab}^{l+1}}$은 다시 위에서 다룬 pooling에 대한 가중치에 chain rule을 적용하고 나면 최댓값 위치인 $(a',b')$ 제외하곤 기울기가 0이라는 사실을 쉽게 알 수 있습니다. 적용하면, $$\sum_{a=0}^{a^{l+1}-1}\sum_{b=0}^{b^{l+1}-1}\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial a_{ab}^{l+1}}\frac{\partial a_{ab}^{l+1}}{\partial w_{ij}^{l+1}}=\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial a_{a'b'}^{l+1}}\frac{\partial a_{a'b'}^{l+1}}{\partial w_{ij}^{l+1}}$$가 됩니다. 위 식의 최우측 기울기인 $\frac{\partial a_{a'b'}^{l+1}}{\partial w_{ij}^{l+1}}$만 정리하면 마무리 할 수 있습니다. $a_{a'b'}^{l+1}$은 $$f\left(z_{a'b'}^{l+1}\right)=f\left(\sum_{m=0}^{m^{l+1}-1}\sum_{n=0}^{n^{l+1}-1}w_{mn}^{l+1}x_{a'+m,b'+n}^{l}\right)$$이이 됩니다. 따라서 다음과 같은 관계를 세울 수 있습니다. $$\frac{\partial a_{a'b'}^{l+1}}{\partial w_{ij}^{l+1}}=\frac{\partial a_{a'b'}^{l+1}}{\partial z_{a'b'}^{l+1}}\frac{\partial z_{a'b'}^{l+1}}{\partial w_{ij}^{l+1}}$$ 우리는 $f$를 Relu로 가정했으니 $z_{a'b'}^{l+1}>0$이라면 $\frac{\partial a_{a'b'}^{l+1}}{\partial z_{a'b'}^{l+1}}=1$일 것이고, $z_{a'b'}^{l+1} \leq 0$ 이면 $\frac{\partial a_{a'b'}^{l+1}}{\partial z_{a'b'}^{l+1}}=0$이 될 것 입니다. 마지막으로 $\frac{\partial z_{a'b'}^{l+1}}{\partial w_{mn}^{l+1}}=x_{a'+m,b'+n}^{l}$를 합성곱 연산의 정의로 부터 쉽게 계산할 수 있습니다. 위 두 가지 부분을 다시 대입하면, $$\frac{\partial L}{\partial w_{mn}^{l+1}}=\frac{\partial L}{\partial o_{1}}\frac{\partial o_{1}}{\partial x_{00}^{l+1}}\frac{\partial x_{00}^{l+1}}{\partial a_{a'b'}^{l+1}}\frac{\partial a_{a'b'}^{l+1}}{\partial w_{ij}^{l+1}}$$
이렇게 모든 가중치의 기울기를 구하고 나면 앞서 살펴본 gradient descent algorithms으로 가중치를 학습할 수 있습니다. $$w^{(t+1)}\leftarrow w^{(t)}-\eta\frac{\partial L}{\partial w^{(t)}}$$ 아주 간단한 예제로 포스팅을 작성했습니다. 본 내용을 토대로 여러층으로 확장 시킬 수 있습니다. 만일 추가적인 내용이 궁금하시다면 댓글에 남겨두시면 추가해보도록 하겠습니다. 이상으로 포스팅을 마치겠습니다.
어떠한 형태의 co-work도 환영합니다.. 연락주세요..ㅎㅎ (공지사항 참고)
'Deep Learning > Convolutional Neural Networks' 카테고리의 다른 글
| VGG-16, VGG-19, 2014 (1) | 2023.02.20 |
|---|---|
| AlexNet, 2012 (0) | 2023.02.10 |
| LeNet-5, 1998 (0) | 2023.01.30 |
| Convolution Neural Networks (합성곱 신경망) (44) | 2019.06.23 |




댓글