데이터 분석 방법론을 공부하다 보면 빈번하게 특이값분해(SVD, Singular Value decomposition)을 마주치게 됩니다. 이번 포스팅에서는 SVD의 정의는 무엇이고, 어떤 이유로 데이터 분석 방법론에서 차원 축소의 관점으로 자주 이용되는지 살펴보도록 하겠습니다.
SVD 정의
SVD는 실수공간과 복소공간에서 정의됩니다. 하지만 여기에서는 실수공간에 국한하여 정의하도록 하겠습니다.
$M$은 $m\times n$ 실수 행렬이라고하면, SVD가 다음의 factorization 형태로 존재합니다. $$M=U\Sigma V^{\top},$$ 여기에서
- $U$: $m\times m$ orthogonal matrix
- $\Sigma$: $m \times n$ diagonal matrix
- $V^{\top}$: $n \times n$ orthogonal marix
입니다. Orthogonal 하다는 것은 행렬의 열벡터간 독립이라는 의미로 다음과 같은 관계가 성립합니다. $$\begin{align*}U^{\top}U&=I_{m}\\V^{\top}V&=I_{n}\end{align*}$$ 여기서 $I$는 단위 행렬이고 아랫 첨자는 정방 행렬의 크기를 의미합니다. 하나 더 짚고 넘어갈 것은 diagonal matrix가 정방이 아니라는 점입니다. $m$, $n$의 크기에 따라서 다음과 같이 정의 됩니다.
- $m>n$ $$\Sigma=\begin{pmatrix}\sigma_{1}&0&\cdots&0\\0&\sigma_{2}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sigma_{m}\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{pmatrix}$$
- $m<n$ $$\Sigma=\begin{pmatrix}\sigma_{1}&0&\cdots&0&0&\cdots&0\\0&\sigma_{2}&\cdots&0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots\\0&0&\cdots&\sigma_{n}&0&\cdots&0\end{pmatrix}$$
SVD 기하학적 의미
벡터에 일반 행렬이 곱해지는 것과 Diagonal matrix가 곱해지는 것이 어떤 의미인지 살펴본 후 확장하여 SVD를 기하학적인 의미로 생각해보기로 하겠습니다.
행렬과 벡터의 곱
어떤 행렬에 벡터를 곱한다는 것은 벡터의 값의 변환을 의미합니다. 여기에서는 SVD를 이해하기 앞서, orthogonal matrix와 diagonal matrix가 어떤 벡터 변환을 행하는지 살펴보겠습니다. 간단한 예제와 함께 보겠습니다. $$M=\left.\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\right|_{\theta=\pi/2}, x=[1, 0]^{\top}$$ 위 $M$, $x$을 고려해보겠습니다. $M$은 널리 알려진 회전 행렬이며, $M^{\top}M=I_{2}$가 되는 orthogonal matrix입니다. 비약해서 설명하면 orthogonal matrix는 회전 행렬입니다. 이제 행렬에 벡터를 곱해 보면, $$Mx=\begin{pmatrix}\cos\frac{\pi}{2}&-\sin\frac{\pi}{2}\\\sin\frac{\pi}{2}&\cos\frac{\pi}{2}\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}=[0, 1]^{\top}$$ 벡터 $x$를 90도 회전 시킴을 확인할 수 있습니다.
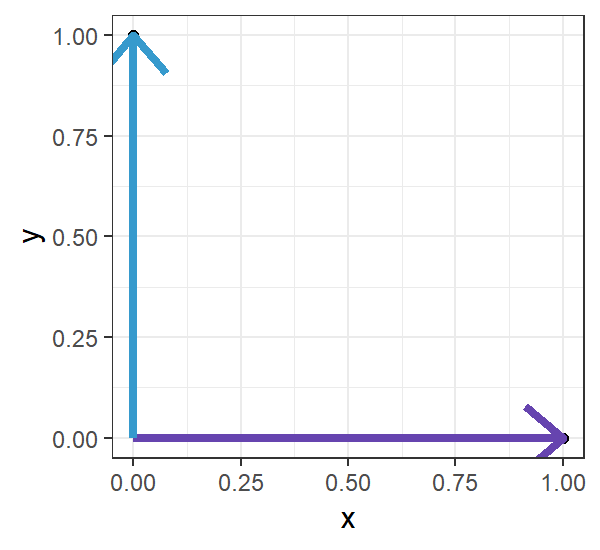
Diagonal matrix는 조금 특이한 형태로 벡터 변환을 합니다. 다음의 Diagonal Matrix를 생각해보겠습니다. $$D=\begin{pmatrix}1&0\\0&2\end{pmatrix}$$ 그리고 이어서 아까 구한 $Mx$ 앞에 곱한, 즉, $DMx$는 다음과 같습니다. $$DMx=[0,2]^{\top}$$ 벡터의 진행방향은 바뀌지 않고, $x$ 방향으로 1배, $y$ 방향으로 2배 크기만 바뀌었다는 사실을 알 수 있습니다.

이렇듯 digonal matrix는 진행방향을 유지하면서 크기만 바꿔주는 역할을 합니다. 이러한 이유로 diagonal matrix의 대각 원소들을 scaling factor라고도 부릅니다.
SVD는 어떤 변환 행렬일까?
행렬 $M$가 $U\Sigma V^{\top}$로 SVD된 것을 고려해보겠습니다. 행렬 $M$에 벡터 $x$를 곱해, $Mx=U\Sigma V^{\top}x$, SVD가 기하학적으로 어떤 의미를 지니는지 순서대로 살펴보면 다음과 같습니다.

- $V^{\top}x$는 $x$를 회전 변환합니다. ($\because$ $V^{\top}$은 orthogonal matrix)
- $\Sigma V^{\top}x$는 앞에 diagonal matrix를 곱해줌으로써 크기를 조절합니다.
- $U\Sigma V^{\top}x$는 회전하고 크기가 조절된 벡터를 다시 회전 시킵니다.
앞에 나온 이야기를 종합하면 직관적으로 이해할 수 있습니다. 위 예제는 정방행렬 $M$을 가정한 것입니다. $M$이 $m\times n$인 경우를 생각해보면, $x\in\mathbb{R}^{n}$인 벡터를 $Mx$ 연산을 취하고 나면, $Mx\in\mathbb{R}^{m}$이 된다는 것을 알 수 있습니다. 즉, 어떤 벡터 dimension을 변환시키는 변환이 SVD입니다. 그렇다면 $U$, $\Sigma$, $V^{\top}$ 각각이 의미하는 바가 중요해집니다. SVD 정의 양변에 $V$를 곱해주면 다음과 같은 관계를 얻을 수 있습니다. $$MV=U\Sigma$$ 좌변부터 살펴보면, $V$는 SVD 정의로 부터 서로 직교하는 열벡터로 구성된 행렬이라고 했습니다. 따라서 $MV$를 계산하고 나면 서로 직교하는 열벡터들을 $M$ 행렬로 변환시킨 벡터의 집합이 됩니다. 우변의 $U$는 이렇게 행렬 $M$에 의해 변환된 벡터들에 크기 변환($\Sigma$)한 결과가 직교하고 차원이 다른 벡터의 집합 $U$로 표현 할 수 있음을 나타냅니다.
SVD 활용
$m<n$에 대한 SVD의 정의를 풀어서 쓰면, $$\begin{align*}M&=\left(u_{1},u_{2},\cdots,u_{m}\right)\begin{pmatrix}\sigma_{1}&\cdots&0&0&\cdots&0\\0&\ddots&0&0&\cdots&0\\0&\cdots&\sigma_{m}&0&\cdots&0\end{pmatrix}\begin{pmatrix}v_{1}^{\top}\\\vdots\\v_{n}^{\top}\end{pmatrix}\\&=u_{1}\sigma_{1}v_{1}^{\top}+\cdots+u_{m}\sigma_{m}v_{m}^{\top}\end{align*}$$가 됩니다. 즉, SVD를 이용하면 분해된 행렬의 합으로 나타낼 수 있습니다. 보통 $\sigma_{m}$은 $\sigma_{1}\geq\sigma_{2}\geq\cdots\geq\sigma_{m}$으로 정리합니다. 이는 행렬 $M$을 분해하고 나면, 직교하는 벡터중 행렬 $M$을 표현할 때가 영향력이 큰 순서대로 정리하기 위함입니다. 그래서 SVD 결과 전체를 이용하지 않고, 어떤 $p<m$에 대해 행렬을 분할(partitioning)하여, $(p\times p)\times(p\times n)\times(n\times n)$ 일부만 이용함으로써 근사된 결과를 얻는 형태로 SVD를 활용할 수 있습니다. $$M=\left(u_{1},u_{2},\cdots,u_{p}\right)\begin{pmatrix}\sigma_{1}&\cdots&0&0&\cdots&0\\0&\ddots&0&0&\cdots&0\\0&\cdots&\sigma_{p}&0&\cdots&0\end{pmatrix}\begin{pmatrix}v_{1}^{\top}\\\vdots\\v_{n}^{\top}\end{pmatrix}$$
$U\Sigma V$를 어떻게 계산할까?
사실 SVD는 Eigen Decomposition의 일반화된 방법입니다. 즉, 정방 행렬에 적용이 가능한 방법을 그렇지 않은 행렬에 적용시킨 것이 SVD입니다. Eigen Decompositon의 내용은 다소 단순하고 구글에서 얼마든지 쉽게 이해가능한 자료를 찾아볼 수 있고, 본 포스팅의 가독성의 위해 생략하였습니다.
이어서 $U\Sigma V$를 얻는 방법을 간단하게 설명하겠습니다. $$M^{\top}M=V\Sigma^{\top}\Sigma V^{\top}\\ MM^{\top}=U\Sigma\Sigma^{\top}U^{\top}$$는 SVD 정의에 의해 계산됩니다. 이것은 Eigen Decomposition 그 자체임을 쉽게 알 수 있습니다. 즉, $M^{\top}M$, $MM^{\top}$에 대해 각각 Eigen Decomposition을 적용하여 $U\Sigma V$를 얻을 수 있습니다.
마치며
SVD를 활용한 여러방법이 있습니다. 본 포스팅은 방법론 설명시 SVD가 있을 때 참조하는 역할로 쓰려고 합니다. 수학 지식이 미천합니다. 혹시라도 잘 못된 부분이 발견되면 얼마든지 댓글로 남겨주시면 감사하겠습니다.
References
- Wikipedia contributors. "Singular value decomposition." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 3 Jul. 2019. Web. 8 Jul. 2019.
- https://wikidocs.net/25820
댓글