CNN 이란?
CNN은 Convolutional Neural Networks의 줄임말로 인간의 시신경을 모방하여 만든 딥러닝 구조 중 하나입니다. 특히 convolution 연산을 이용하여 이미지의 공간적인 정보를 유지하고, Fully connected Neural Network 대비 연산량을 획기적으로 줄였으며, 이미지 분류에서 좋은 성능을 보이는 것으로 알려져있습니다.
CNN의 간단한 역사
시신경의 구조
David H. Hubel과 Torsten Wiesel은 1959년 시각 피질에 구조에 대한 고양이 실험을 수행했습니다. 실험에서 시각 피질 안의 많은 뉴런들이 작은 local receptive field를 가진다는 사실을 밝혀냈습니다. Local의 의미는 보이는 것 중 일부 범위 안에 있는 시각 자극에만 반응한다는 의미입니다. 여러 local receptive field의 영역은 서로 겹칠 수 있고, 이를 합치면 전체 시야를 감싸게 됩니다. 특히 simple cell은 직선에만 반응한다는 것과 complex cell은 더 큰 수용소를 가지고 있어 더 복잡한 패턴에 반응함을 보였습니다.
Neocognition
Hubel과 Wiesel의 연구에 영감을 받아, 1980년 Kunihiko Fukushima는 Neocognition을 발표하는데 이는 CNN 구조의 시초라고 할 수 있습니다. Neocognition의 논문에서는 convolutional layer와 down sampling layer를 제안했습니다.
LeNet-5
1998년Yann LeCun, Leon Bottu, Yoshua Bengio, Patrick Haffner가 수표에 쓰인 손글씨 숫자를 인식하는 딥러닝 구조 LeNet-5를 발표하며 현대 CNN의 초석이 되었습니다.
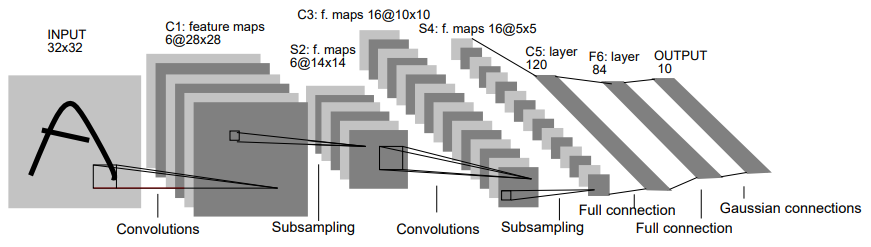
이어서 CNN의 핵심이 되는 convolutional layer, pooling layer에 대해서 자세히 살펴 보도록 하겠습니다.
Image Data
먼저 이미지를 정형 데이터화하는 방법을 생각해보겠습니다. 정형 데이터화라는 말은 컴퓨터로 식별가능한 형태로 데이터를 변환하는 것을 의미합니다. 예를 들어, 남자/여자라는 내용이 있으면, 남자를 0, 여자를 1로 하겠다와 같은 약속을 정형화한다고 합니다. 이미지는 픽셀 단위로 구성이 되어 있고, 각 픽셀은 RGB 값으로 구성되어 있습니다. 즉 아주 작은 색이 담긴 네모 상자가 여러개가 모여 이미지가 되며, 색은 R(빨강), G(초록), B(파랑)의 강도의 합으로 표현할 수 있습니다. 이미지를 정형 데이터화 하는 것 방법 중 하나는 흑백 이미지의 경우 '가로x세로'에 흑색의 강도가 들어간 배열로, 컬러 이미지의 경우 '가로x세로x3'의 배열로 나타낼 수 있으며 마지막 3에는 각각 R, G, B의 강도의 값으로 구성할 수 있습니다.

이미지 해상도 외에 겹쳐지는 부분을 Channel(채널)이라고 하며, 흑백의 경우 1, 컬러의 경우 3입니다. (RGBA의 경우 4이며 마지막 A는 이미지의 밝기인 Alpha)
Convolutional Layer (합성곱 층)
Convolutional Layer 가 왜 필요할까?
왜 convolutional layer가 필요할까? 먼저 3x3 흑백이미지를 고려해보겠습니다. (단순히 구분을 위해 색을 칠해두었습니다.)

다음과 같은 3x3 이미지를 고려해보겠습니다. 우리가 일반 딥러닝 구조로 이미지를 분석한다는 것은 3x3 배열을 오른쪽처럼 펼처서(Flattening)하여 각 픽셀에 가중치를 곱하여 은닉층으로 연산 결과를 전달하는 것과 같습니다. 이미지의 특성상 각 픽셀 간에 밀접한 상관 관계를 가지고 있을 텐데, flattening해서 분석하면 데이터의 공간적구조를 무시한다는 것을 쉽게 알 수 있습니다. 이미지 데이터의 공간적인 특성을 유지하는 것이 convolutional layer의 등장에 큰 동기가 되었습니다. 이어서 convolution이 어떤 연산인지 알아보고 딥러닝에 어떻게 녹여냈는지 순차적으로 살펴보겠습니다.
Convolution (합성곱) 이란?
Convolution은 두 함수($f$, $g$)를 이용해서 한 함수($f$)의 모양이 나머지 함수 ($g$)에 의해 모양이 수정된 제3의 함수 ($f*g$)를 생성해주는 연산자로 통계, 컴퓨터 비전, 자연어 처리, 이미지 처리, 신호 처리 등 다양한 분야에서 이용되는 방법입니다. Convolution의 정의는 다음과 같습니다. $$\left(f*g\right)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau$$ Convolution의 정의를 그대로 이해하면, y축 기준 좌우가 반전이된 함수 $g$를 우측으로 $t$만큼 이동한 함수 $g(t-\tau)$와 $f(\tau)$를 곱해진 함수의 적분입니다. 예제를 살펴보겠습니다. 다음 두 함수 $f$, $g$를 고려하겠습니다.

함수 $f$, $g$는 $f(t)=I\left(t\in[0,1]\right)$, $g(t)=tI\left(t\in[0,1]\right)$입니다. 먼저 $t=3$인 경우를 생각해보겠습니다.
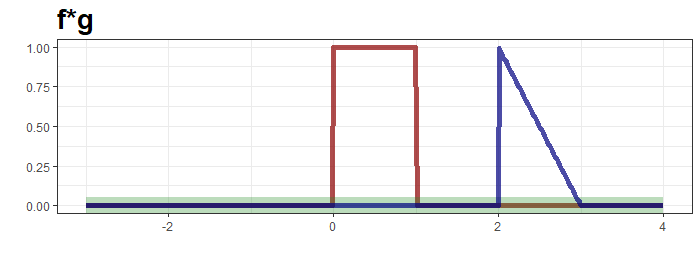
빨간 선 $f$는 고정된 것과 파란선 $g$를 y축 대칭시킨뒤 우측으로 3만큼 이동한 것을 볼 수 있는데, 이 때 두 함수를 곱한 것이 적분 대상이 되며 초록 띠와 대응됩니다. 초록띠와 x축으로 둘러 쌓인 면적이 0임으로 $t=0$의 convolution은 0이 됩니다. $t=0.5$일 때는 다음과 같습니다.

초록띠와 x축으로 둘러 쌓인 면적은 0.25로 $t=0.5$에서 convolution결과입니다. $t$를 $-\infty$ 부터 $\infty$까지 순차적으로 살펴보면 다음과 같습니다.
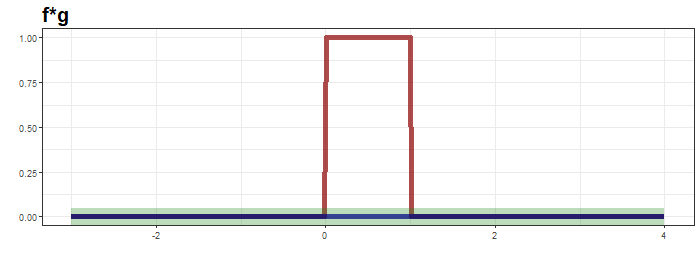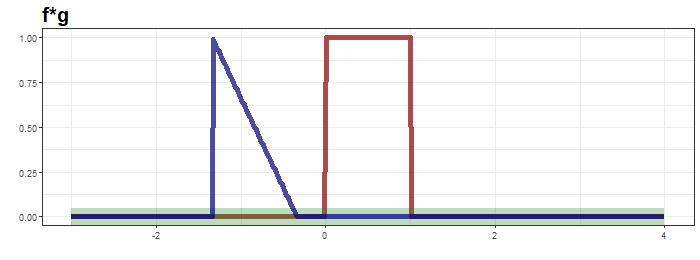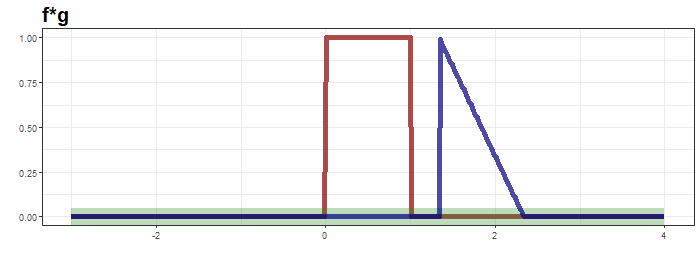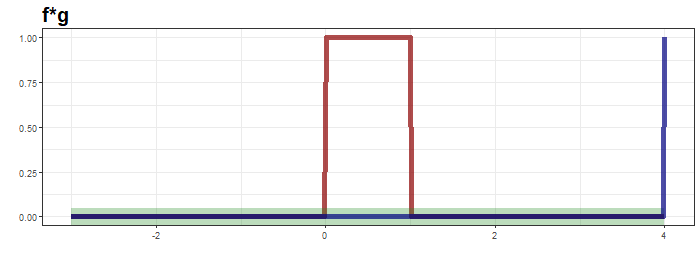
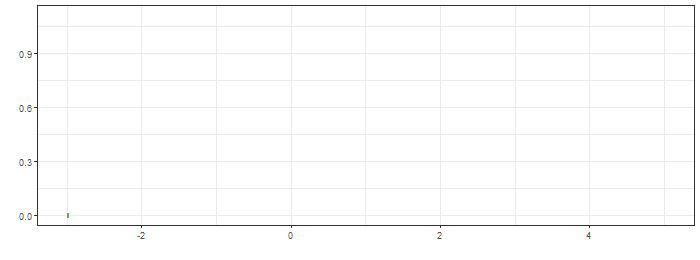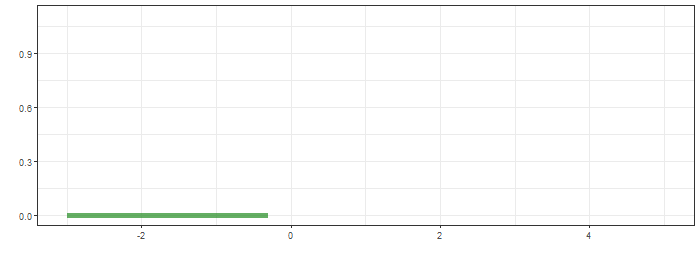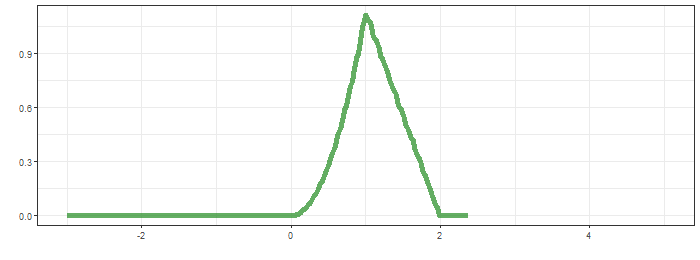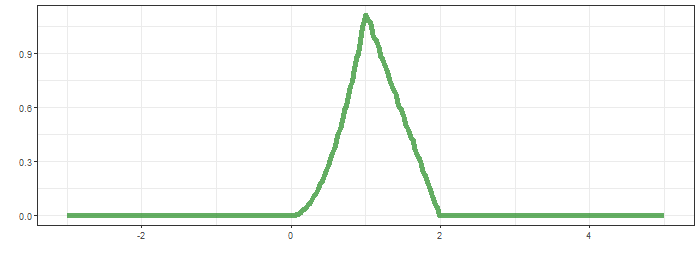
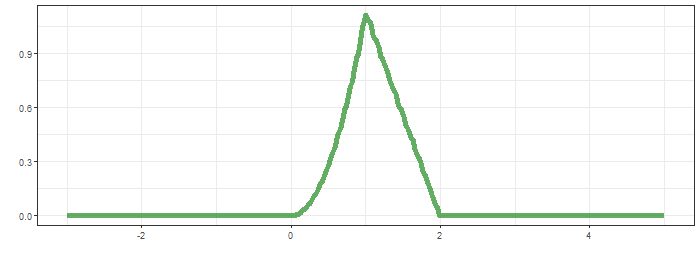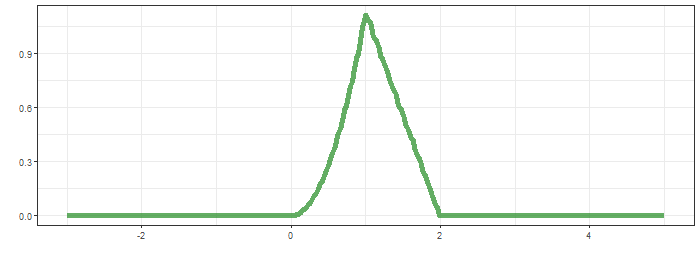
최상단의 그림은 함수 $g$가 이동하면서 연산의 적분 대상함수의 모습을, 가운데는 convolution 결과가 순차적으로 생성되는 과정을, 마지막은 $f*g$의 결과입니다.
추가적으로 Cross-correlation이 있습니다. Cross-correlation은 $$(f*g)(t)\int_{-\infty}^{\infty}f(\tau)g(t+\tau)$$입니다. $g$에서 y축 반전을 거치지 않는 것이 convolution과의 차이입니다. 비교해서 살펴보면 아래와 같습니다.
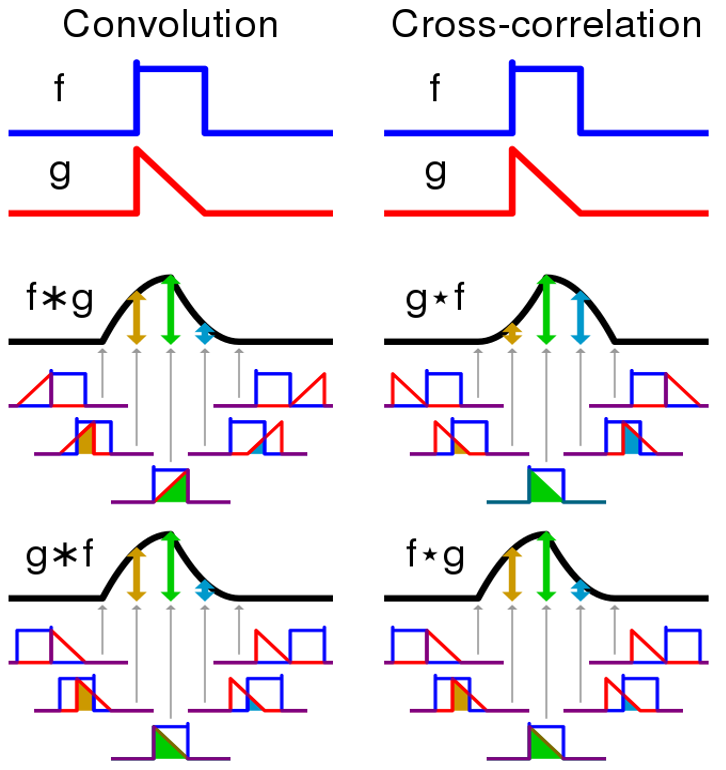
Convolutional Layer의 연산법은 정확하게는 cross-correlation입니다. 하지만 CNN에서는 가중치를 학습하기 때문에 convolution과 cross-correlation을 정확히 구분 할 필요가 없습니다. 이제 본격적으로 CNN을 살펴보겠습니다.
Convolutional Layer (합성곱 층)
Convolutional layer는 아래 그림과 같이 빨간 상자를 sliding window 방식으로 가중치와 입력값을 곱한 값에 활성함수를 취하여 은닉층으로 넘겨줍니다.
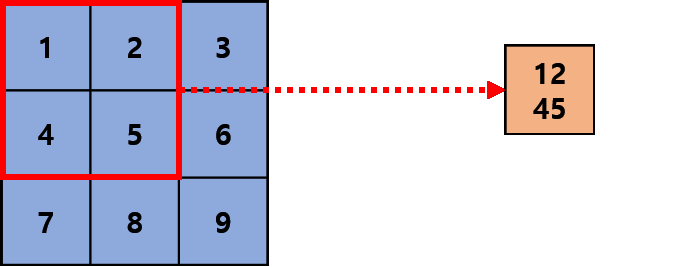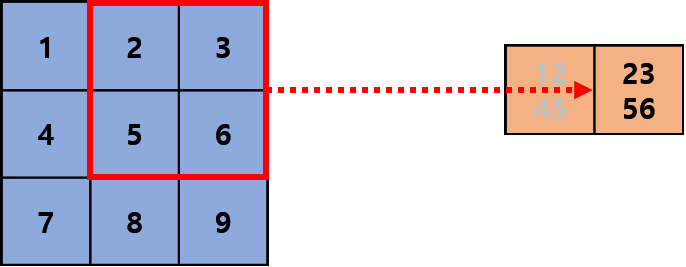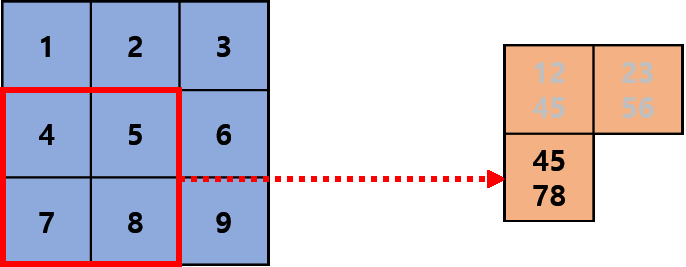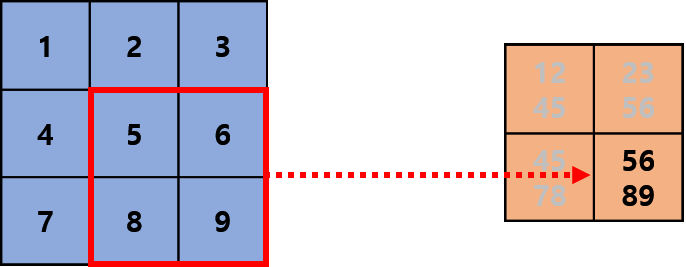
Convolutional layer는 사람이 실제로 보는 것을 우측의 파란 3x3 픽셀이라고 했을 때, 전체를 인식하는 것이 아니라, 일부분을 빨간색 상자에 투영하고 그를 우측의 주황색 수용역역(receptive field)에 연결되어 복합적으로 해석하는 것을 모방한 것입니다. 이어서 실제로 딥러닝 프레임워크에서 어떻게 연산이 이뤄지는지 살펴보겠습니다.
Convolutional Layer 계산방법 개요
예제를 이용해서 이해하는 것이 가장 빠르기 때문에 아래 예제 하나를 고려하겠습니다.
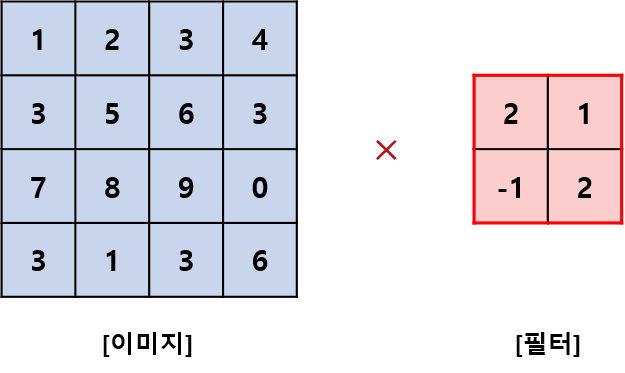
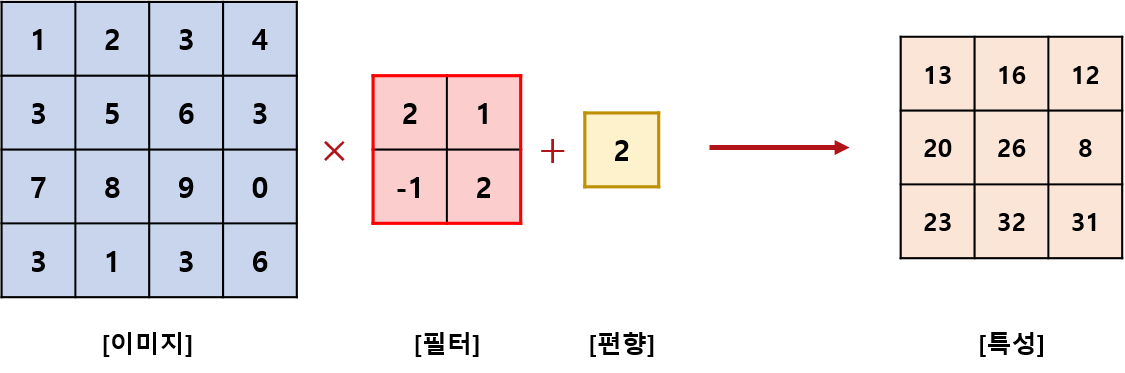
위 그림의 좌측은 흑백 이미지의 픽셀 값이고, 우측은 좌측의 이미지를 투영하여 convolution (합성곱 연산)을 하는 것으로 필터(filter) 혹은 커널 (kernel) 또는 윈도우 (window)라고 부릅니다.
딥러닝 프레임워크 관점에서 다시 말하면, 픽셀 값은 입력 값 (input)이 되고, 필터 값은 가중치 (weight)가 됩니다. 이제 연산이 어떻게 이루어지는지 살펴보겠습니다.
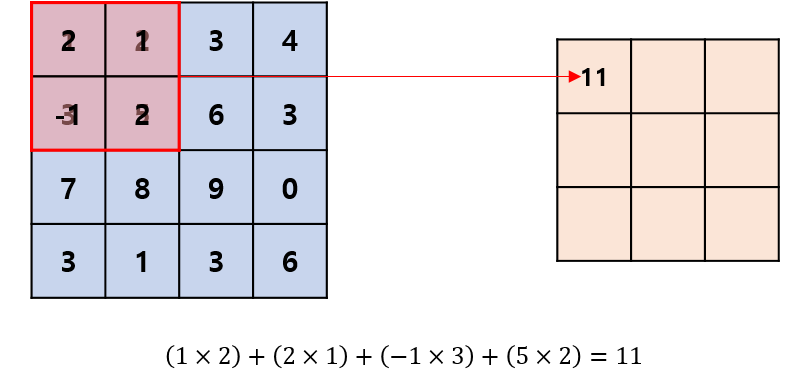
사실 아주 간단합니다. 이미지 좌상단에 이미지와 필터를 포개 놓고, 대응되는 숫자끼리 곱한 뒤, 모든 숫자를 더해주면 됩니다. 이어서 Figure 6 처럼 필터를 sliding window 방식으로 이동해가며 합성곱 연산을 수행하면 됩니다.
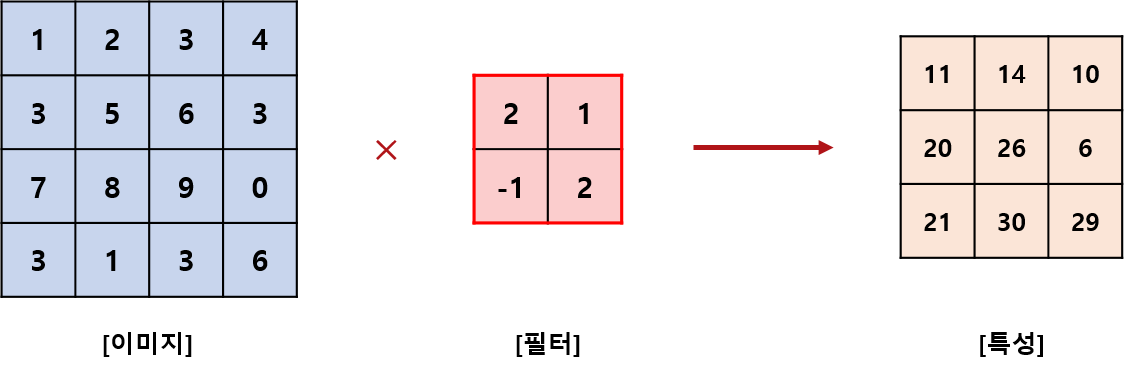
합성곱 연산의 결과를 특성 (feature)라고 부릅니다. 눈치 채셨겠지만 위 예제 기준으로 만약 이미지를 Flattening한다면 특성 1개 마다, 16개 가중치를 학습해야 될 것입니다. 보시다시피 convolutional layer를 도입하며 학습할 가중치가 4개로 줄었고, 컴퓨터 연산의 수를 획기적으로 감소시켰습니다.
인공신경망 포스팅에서 가중치에는 편의(bias)를 더해주엇듯이 Convolutional Layer에서도 편향을 더해주기도 합니다.
Convolutional Layer의 convolution 과정은 입력데이터의 일부만 은닉층으로 연결되는데 이를 local connectivity라고 합니다. Convolutional Layer를 인공신경망의 구조로 풀어서 생각해보겠습니다.
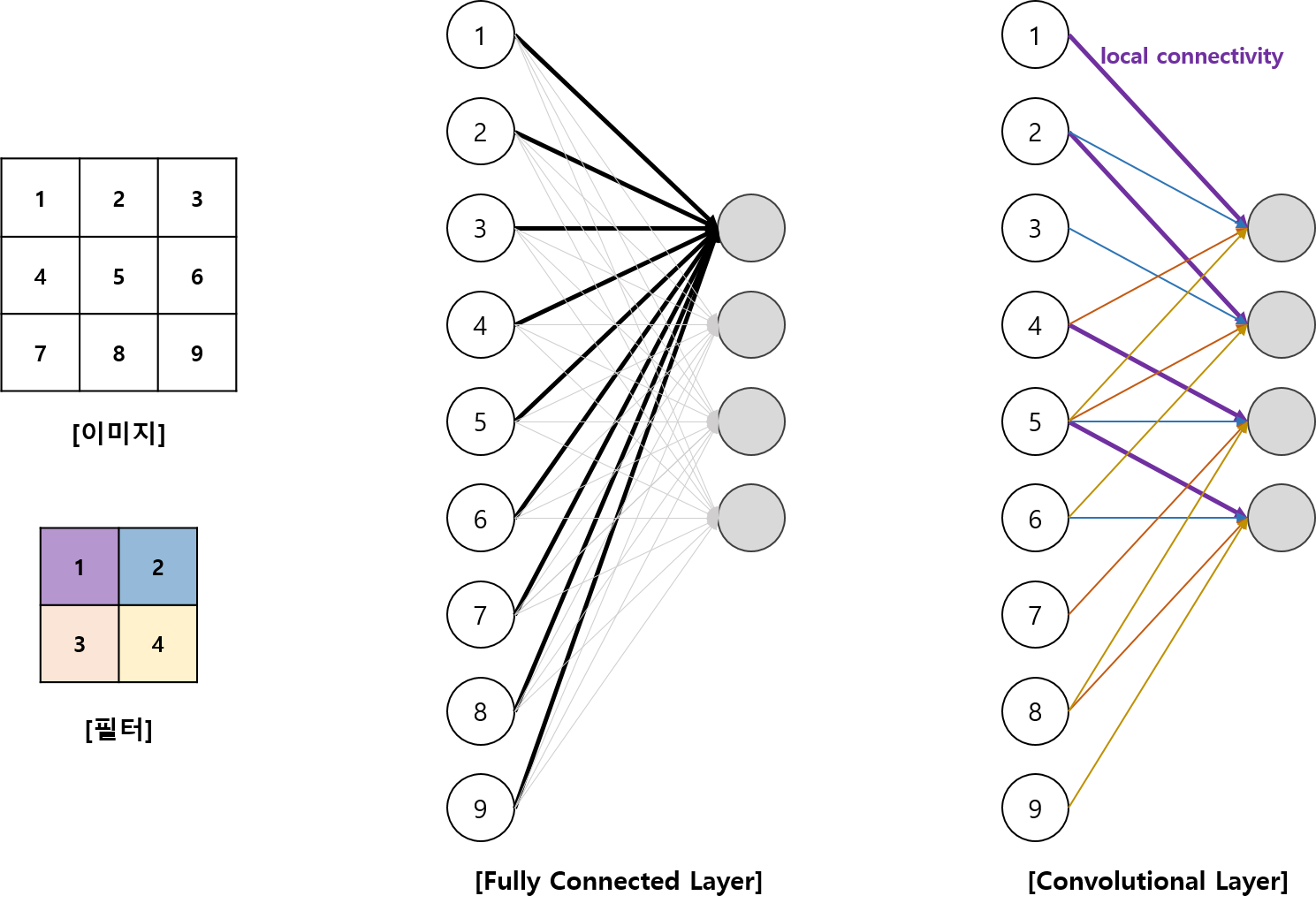
3x3 이미지에 2x2 필터 (스트라이드 1)를 이용한 합성곱과 노드 4의 fully connected layer와 비교한 그림입니다. Fully connected layer에서는 노드별로 다른 가중치 벡터($9\times 4$개 가중치 필요)가 할당되는 반면, convolutional layer에서는 같은 가중치($4$개의 가중치 필요)로 4개의 노드를 계산합니다. 즉, 픽셀의 일부만 연결하고 (local connectivity), 같은 가중치 (sharing weight)를 여러번 사용하여, 계산량을 줄이게됩니다.
지금까지 아주 간단한 합성곱 연산에 대해서 살펴보았는데,
- 필터를 꼭 한 칸씩 이동해야 되는가?
- convolution을 반복적으로 수행하면 특성 배열의 크기가 점점 작아지지 않을까?
- 컬러 이미지는 어떻게 convolution을 할 수 있을까?
위와 같은 질문이 가능할 것 입니다. 순서대로 살펴보겠습니다.
Stride (스트라이드)
필터를 입력데이터나 특성에 적용할 때 움직이는 간격을 스트라이드(Stride)라고 합니다.

Padding (패딩)
패딩은 반복적으로 합성곱 연산을 적용했을 때 특성의 행렬의 크기가 작아짐을 방지하는 것과 이미지의 모서리 부분의 정보손실을 줄이고자 이미지 주변에 0으로 채워넣는 방법입니다.
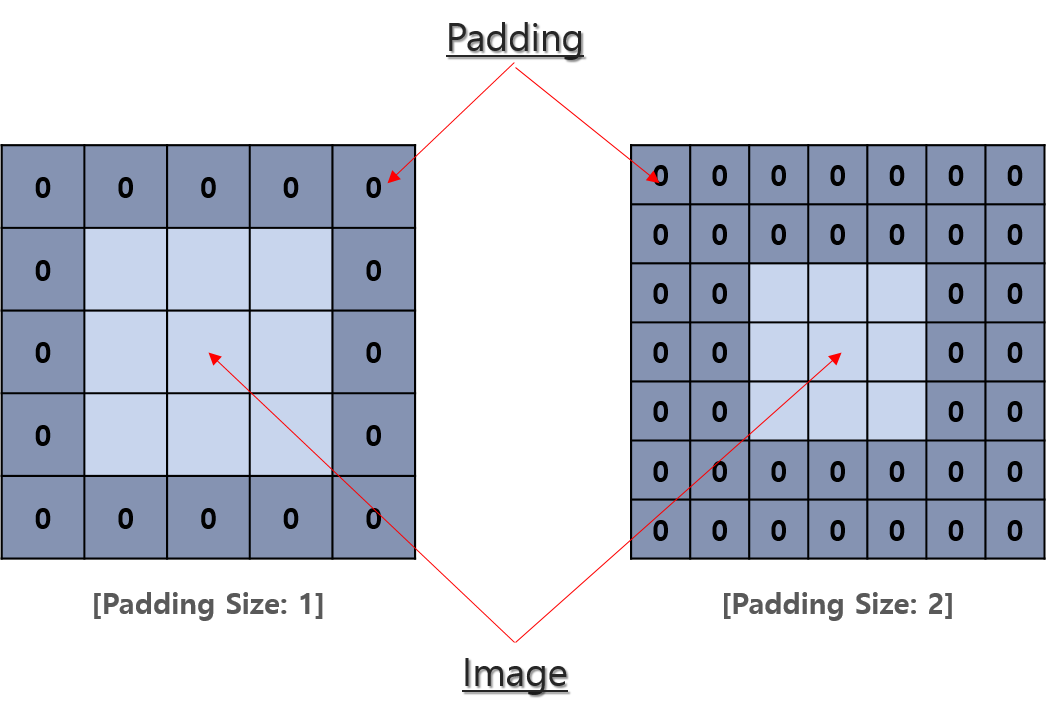
앞의 예제(Figure 9~10)만 보더라도 직관적으로 특성 행렬의 크기가 작아지는 것을 알 수 있습니다. 모서리 정보 손실 발생은 다음과 같이 이해할 수 있습니다.
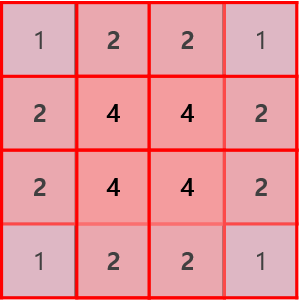
Figure 14은 좌상단부터 필터를 끝까지 이동 시켰을 때 각 픽셀이 이용된 횟수를 체크한 그림입니다. 이미지의 중심부는 4회로 많이 충분히 이용되었지만, 모서리 부분의 픽셀들은 상대적으로 이용횟수가 적음을 알 수 있습니다. 패딩처리를 하고나면 이미지의 모든 부분이 중심부처럼 합성곱 연산에 반영되어 정보 손실을 줄일 수 있습니다.
컬러 이미지 합성곱
컬러 이미지 합성곱에 대해서 살펴보겠습니다.
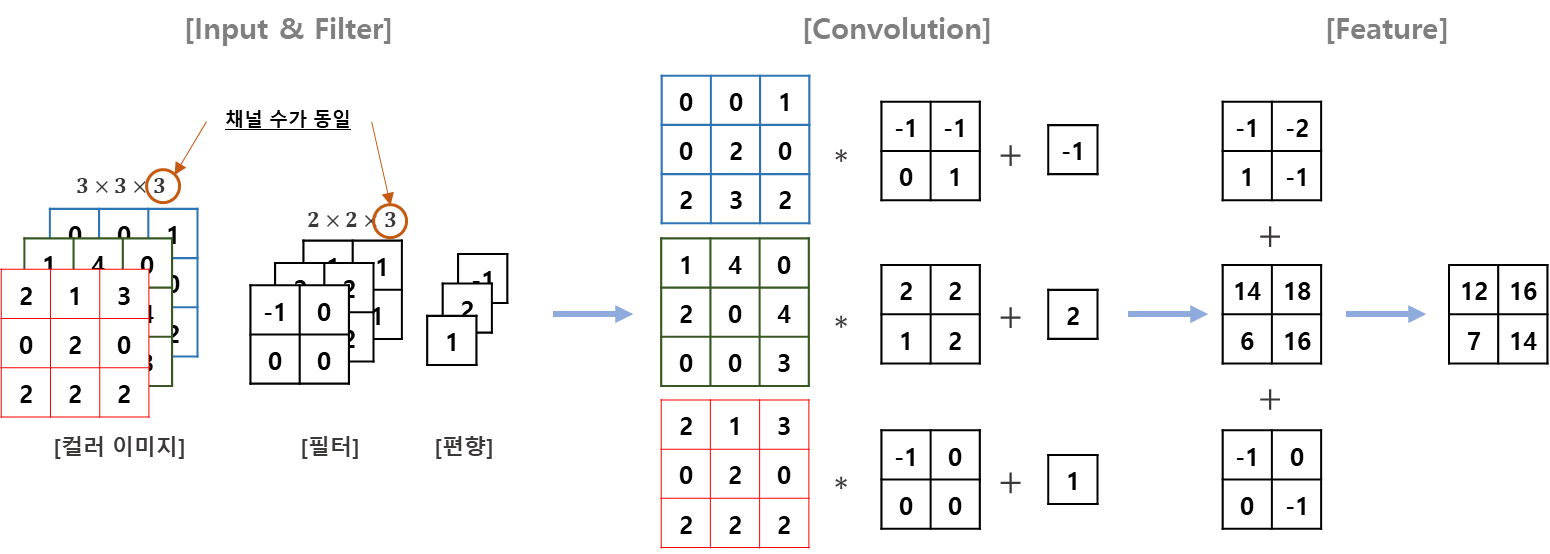
앞서 다룬 흑백이미지와 구분되는 특징이 두 가지가 있습니다. 첫째는 필터의 채널이 3이라는 점이라는 것과 둘째로는 RGB 각각에 다른 가중치로 convolution을 하고 결과를 더해준다는 점입니다. 나머지 스트라이드 및 연산하는 방법은 동일합니다. 여기에서 주의해야할 점은 필터 채널이 3이라고 해서 필터의 수가 3개가 아니라 1개라는 점입니다.
필터 개수가 2이상인 합성곱
지금까진 필터 1개짜리 합성곱에 대해 살펴보았습니다. 필터가 2개 이상이 되면 각각은 특성추출결과의 채널이 됩니다.
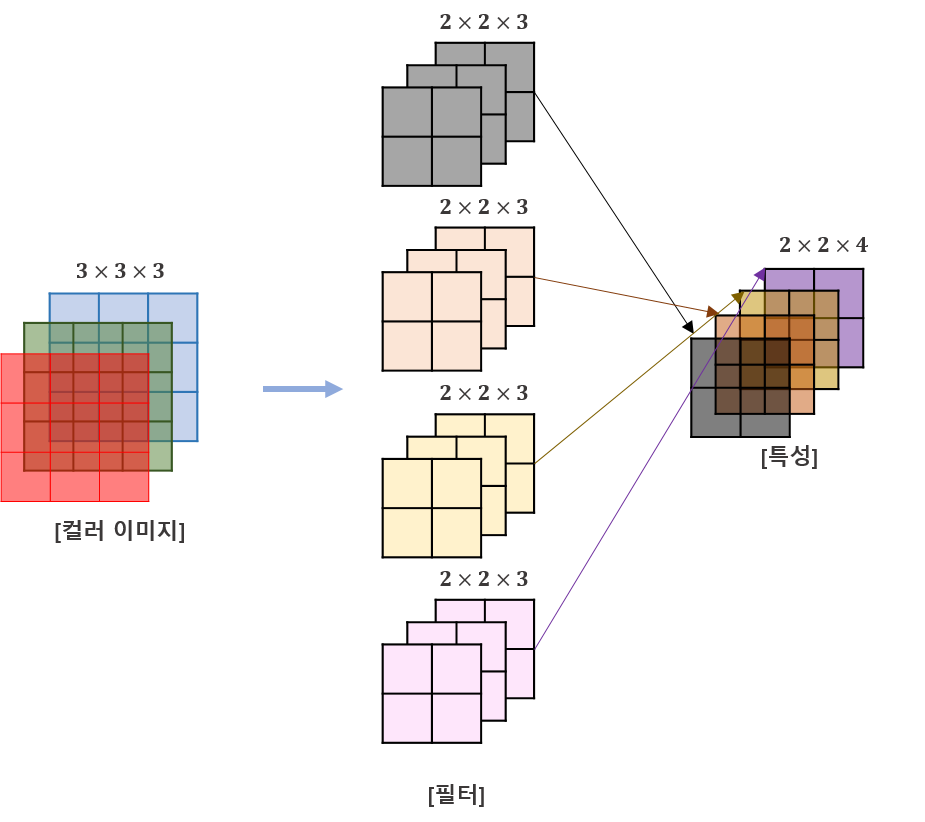
각각을 계산하는 방법은 동일합니다.
합성곱 정리
지금까지 정리한 내용을 간단하게 요약하도록 하겠습니다. 한 층의 합성곱을 일반화 시켜보도록 하겠습니다. 아랫첨자 1, 2는 각각 입력과 출력입니다.
- 입력 데이터: $W_{1}\times H_{1}\times D_{1}$ ($W_{1}$: 가로, $H_{1}$: 세로, $D_{1}$: 채널 또는 깊이)
- Hyper Parameters:
- 필터의 수: $K$
- 필터의 크기: $F$ (정방을 가정)
- 스트라이드: $S$
- 패딩: $P$
- 출력데이터 :
- $W_{2}=(W_{1}-F+2P)/S+1$
- $H_{2}=(H_{1}-F+2P)/S+1$
- $D_{2}=K$
- 가중치의 수: $\left[F^{2}\times D_{1} + D_{1}\right]\times K$
1D Convolution v.s. 2D Convolution v.s. 3D Convolution
합성곱은 이동하는 방향의 수에 따라서 1D, 2D, 3D로 분류할 수 있습니다.
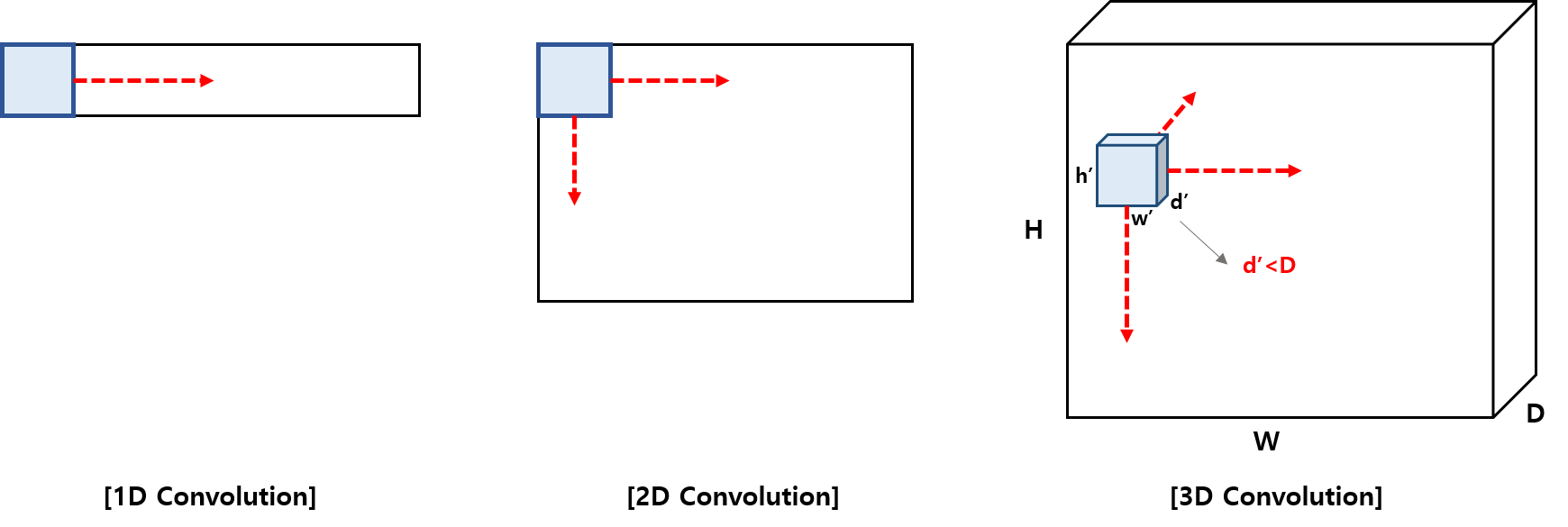
Tensorflow 혹은 Keras에는 convolution 함수로 1d, 2d, 3d 함수가 구분 되어있습니다. 오해하기 쉬운 부분이 1d, 2d, 3d가 입력데이터에 따른다고 생각하는 것입니다. 앞서 말했듯 1d, 2d, 3d는 필터의 진행 방향의 차원 수를 의미합니다.
Figure 15를 살펴보면 컬러 이미지이고 필터 방향이 오른쪽, 아래 방향 두 개이기 때문에 2d convolution이 됩니다. 그렇다면 3d convolution은 어떻게 적용이 될까요? Figure 16을 보면 필터가 4개이고, 이에 따라 출력행렬의 채널 수가 4가 됩니다. 여기에는 채널이 4보다 작은 필터를 적용하여 오른쪽, 아래, 뒤쪽 3 방향으로 3d convolution을 적용할 수 있습니다.
Pooling Layer (풀링층)
풀링층(또는 down sampling)은 데이터의 공간적인 특성을 유지하면서 크기를 줄여주는 층으로 연속적인 합성곱층사이에 주기적으로 넣어줍니다. 데이터의 공간적인 특성을 그대로 유지하면서 크기를 줄여, 특정위치에서 큰 역할을 하는 특징을 추출하거나, 전체를 대변하는 특징을 추출할 수 있다는 장점이 있습니다. 또한, 크기가 줄어들어 학습할 가중치를 크게 줄이게 되고, 이는 과적합 문제(overfitting problem)해결에도 도움이 됩니다. 풀링은 주어진 픽셀에서 값을 추출하는 방식에 따라서 Max Pooling과 Average Pooling으로 구분할 수 있습니다.
Max pooling은 Pooling Filter 영역에서 가장 큰 값을 추출하는 Pooling 방법입니다.
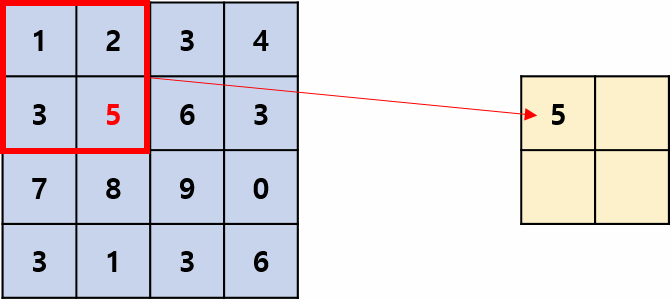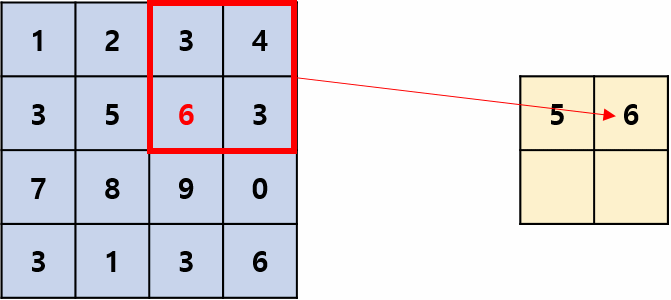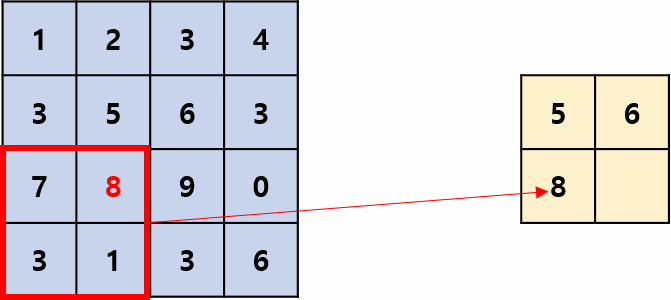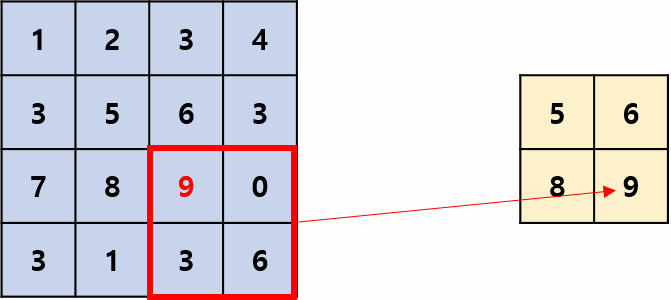
합성곱에서 필터처럼 정해진 스트라이드로 움직이며 위 그림의 스트라이드는 2입니다.
이어서 Average Pooling은 Max Pooling과 다르게 선택된 영역 값의 평균을 추출하는 Pooling 방법입니다.
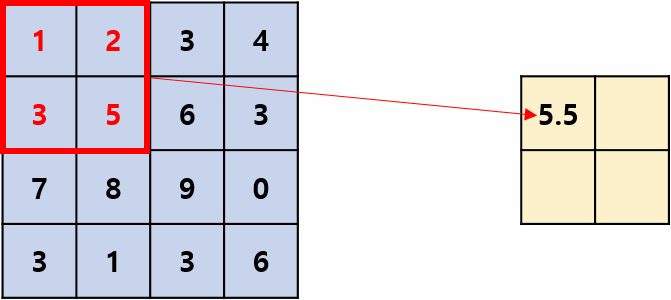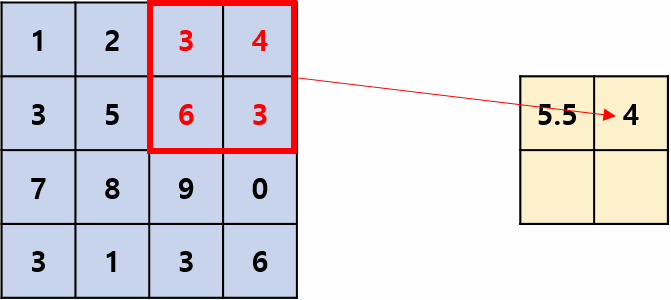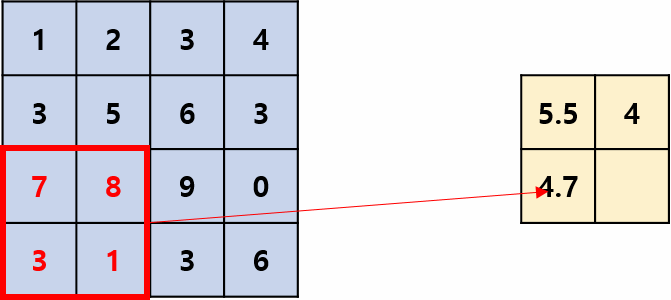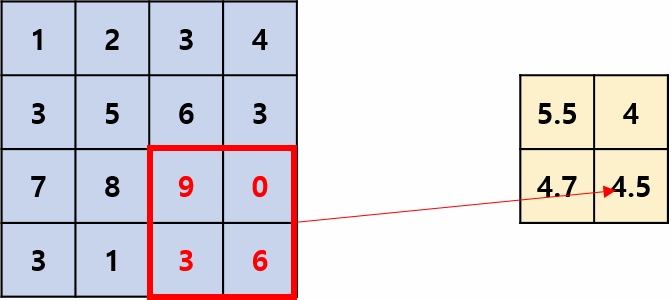
실제 CNN을 적용할 때는 압도적으로 Max Pooling이 많이 이용되며 Average Pooling은 잘 안쓰입니다. (Max Pooling을 이용한 결과가 더 좋다고 합니다.)
Max Pooling과 Average Pooling을 요약하면,
- 입력데이터: $W_{1}\times H_{1}\times D_{1}$
- Hyper Parameters:
- 필터크기: $F$ (정방을 가정)
- 스트라이드: $S$
- 출력데이터:
- $W_{2}=(W_{1}-F)/S+1$
- $H_{2}=(H_{1}-F)/S+1$
- $D_{2}=D_{1}$
Flattening Layer
마지막으로 Flattening layer에 대해서 살펴보겠습니다. 사실 figure 3에서 이미 flattening layer에 대해서 살펴보았습니다.

Flattening Layer의 목적은 Convolutional Layer, Pooling layer를 feature를 추출한 다음에는 추출된 특성을 Output layer에 연결(fully connected layer)하여 어떤 이미지인지 분류하기 위함입니다. 즉, flattening layer 이후로는 일반 신경망 모형과 동일합니다.
정리하며
여기에서는 CNN의 모티브가 된 Hubel & Wiesel의 실험부터 Convolution이 어떤 것 인지, 딥러닝의 convolutional layer는 fully connected layer와 비교하여 어떤 의미가 있는지, Pooling이 어떤 것인지를 살펴보았습니다. 본 블로그의 처음부분에 LeNet-5의 딥러닝 구조가 이제는 쉽게 이해될 것 입니다.
첨언하면 CNN은 기본골격으로 input → padding → convolutional layer → pooling → convolutional layer → pooling → ... → flattening → output의 순으로 진행됩니다. AlexNet이나 LeNet-5 같은 초기 CNN 모형을 살펴보는 것이 CNN을 이해하는데 큰 도움이 될 것입니다. (시간이 나는데로 포스팅할 예정입니다.)
감사합니다:)
References
- Géron, Aurélien. Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems. " O'Reilly Media, Inc.", 2017.1
- Wikipedia contributors. "Convolution." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 24 Jun. 2019. Web. 27 Jun. 2019.
- LeCun, Yann, et al. "Gradient-based learning applied to document recognition." Proceedings of the IEEE 86.11 (1998): 2278-2324.
- http://cs231n.github.io/convolutional-networks
'Deep Learning > Convolutional Neural Networks' 카테고리의 다른 글
| VGG-16, VGG-19, 2014 (0) | 2023.02.20 |
|---|---|
| AlexNet, 2012 (0) | 2023.02.10 |
| LeNet-5, 1998 (0) | 2023.01.30 |
| CNN 역전파 (Backpropagation for CNN) (6) | 2019.07.02 |




댓글